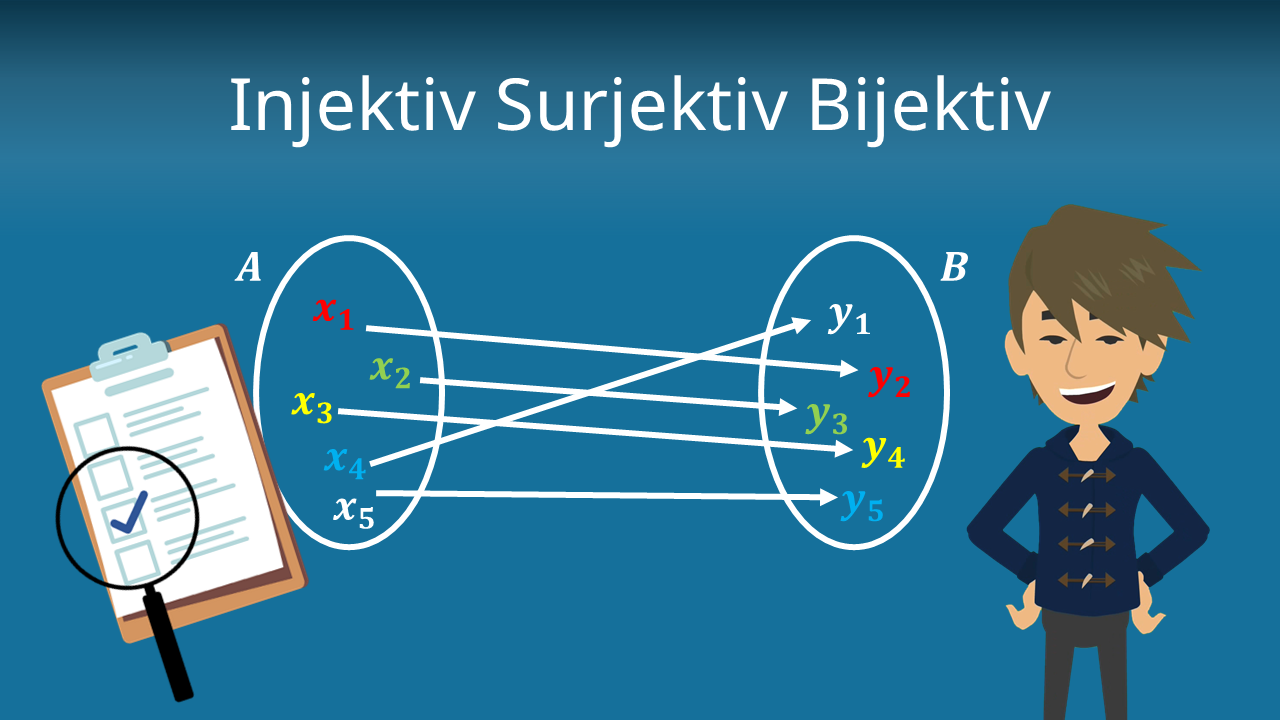
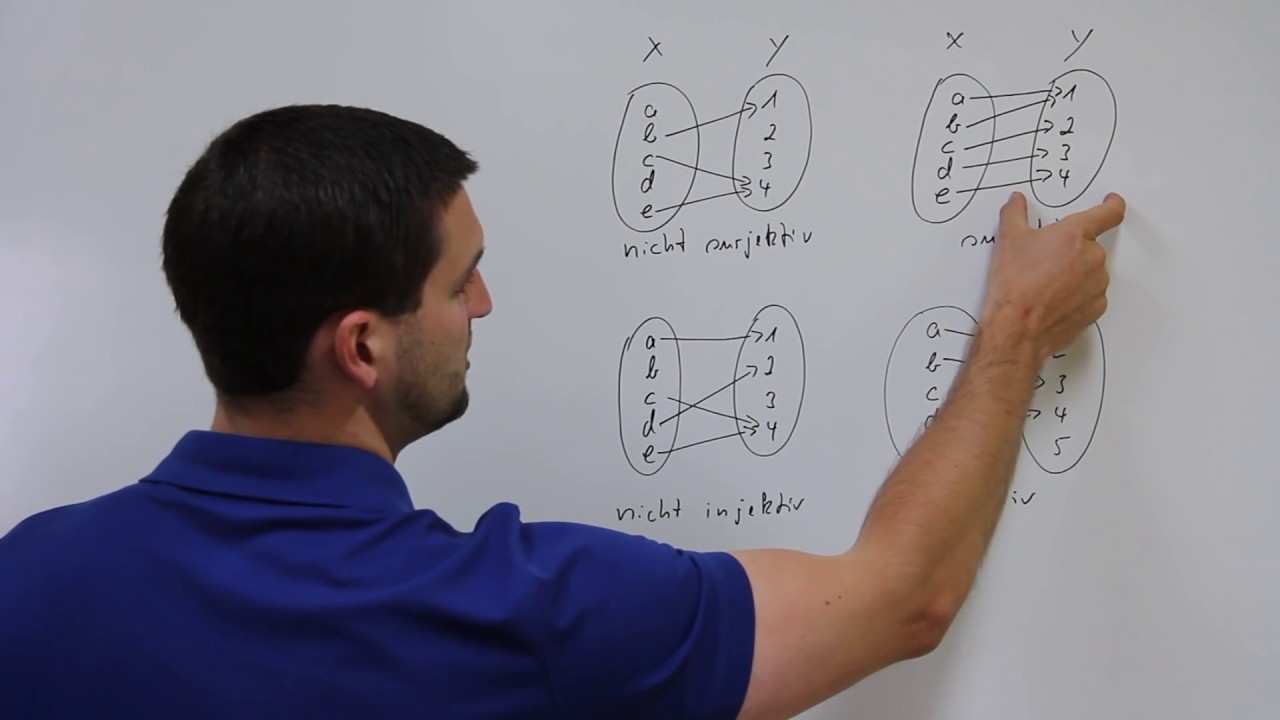
Surjektivitaet Beweisen Beispiel

Bijektive funktion f beispiel.

Surjektivitaet beweisen beispiel. R r f x x3 bijektiv. F ur y y w ahlen wir x y 1. Mein frage ist was ändert sich wenn es ich es bei f. Ein paar beispiele mit r sind die reellen zahlen gemeint mit r die positiven reellen zahlen und die 0.

Nehmen wir als beispiel die funktion z z h x x 5. 2 1 5 1 0 5 0 0 5 1 1 5 2 0 0 5 1 1 5 2 2 5 3 3 5 4 f. Hallo ich habe grundsätzlich ein problem surjektivität zu beweisen. Um surjektivität oder injektivität zu widerlegen reicht ein einziges gegenbeispiel.

Die funktion die jedem studenten einen geburtsmonat zuweist ist surjektiv. R 0 f x x2 surjektiv nicht injektiv. Die quadratische funktion f 2 x x 2 f 2 x x 2 f 2 x x 2 ist nicht surjektiv auf r r r denn negative zahlen werden nicht als funktionswerte angenommen. In abbildung 12 7 ist die funktion f.

Ich hab die aufgabe zu beweisen dass die lineare funktion f. X y bijektiv. Beispiele die lineare funktion f 1 x x f 1 x x f 1 x x ist surjektiv auf r domr r. Ist es dann immer noch injektiv und surjektiv.

Daraus können wir nach dem. Um surjektivität zu beweisen zeigt man dass zu jedem y aus b mindestens ein x aus a mit f x y existiert. Sind zwei funktionen und surjektiv so gilt das auch für die komposition verkettung. In in für die gleiche funktion beweisen soll.

Ir ir mit f x 7x 4 injektiv und surjektiv ist. Dort haben wir festgestellt dass im d r x displaystyle operatorname im d mathbb r lbrack x rbrack. Also ist f bijektiv. R 0 f x exp x injektiv nicht surjektiv.

2 1 5 1 0 5 0 0 5 1 1 5 2 0 1 2 3 4 5 6 7 8 f. 1 0 8 0 6 0 4 0 2 0 0 2 0 4 0 6 0 8 1 1 0 8 0 6 0 4 0 2 0 0 2 0 4 0 6 0 8 1 f. Die funktion f.

Ich weiß und ahne dass sie surjektiv ist aber ohne den gelesenen beweis hätte ich keine idee dies zu beweisen. Es gelte f x1 f x2 x1 1 x2 1 x1 x2 f ist surjektiv. Das hab ich hinbekommen und ist nicht meine frage. Da jedes folgenglied im intervall liegt sind die folgen auch beschränkt.

Dann gilt f x f y 1 y 1 1 y.