Satz Des Pythagoras Beispiel

A 2 b 2 c 2 a2 b2 c2.

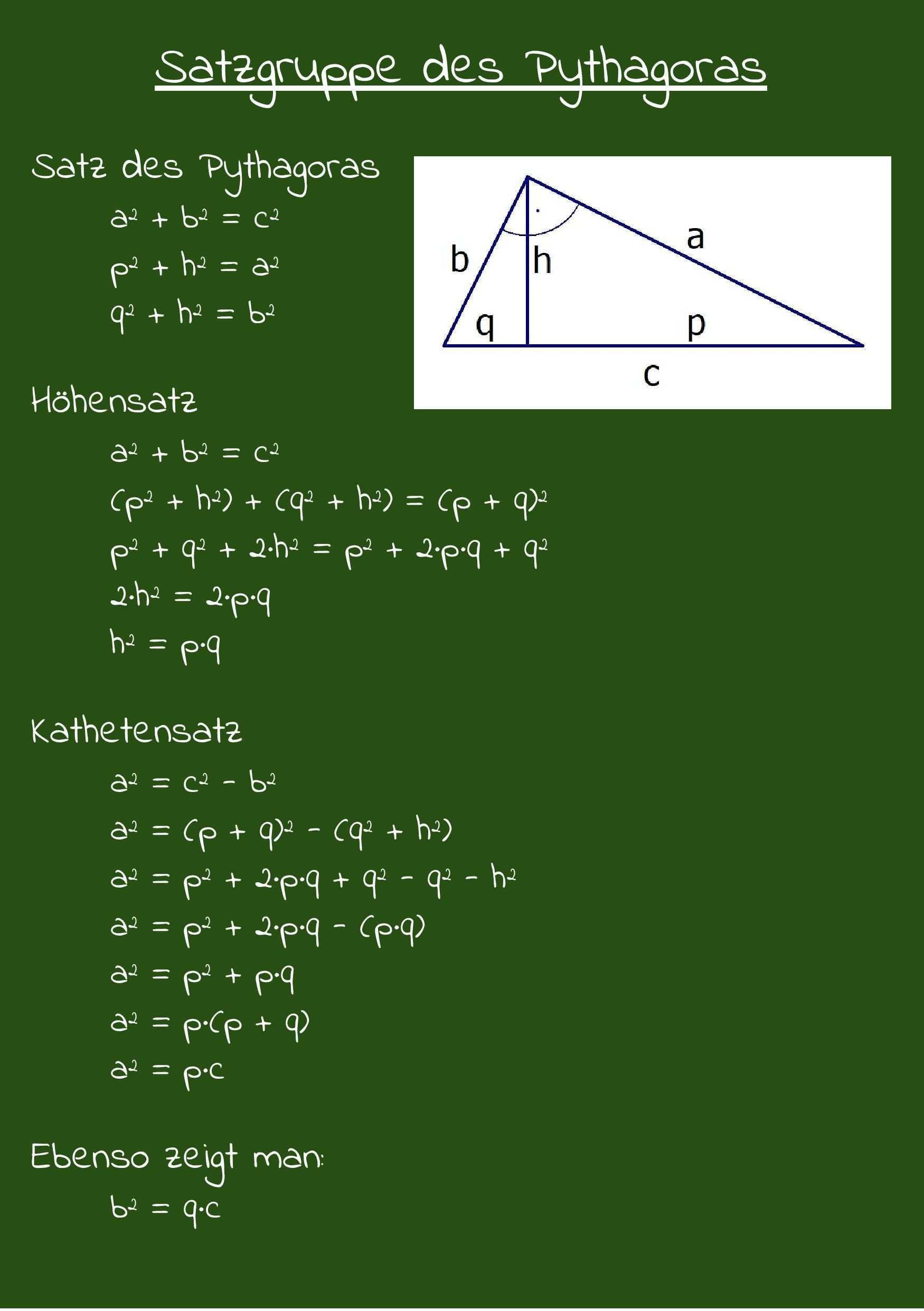
Satz des pythagoras beispiel. C 2 169. A 2 b 2 c 2. Displaystyle a 2 b 2 c 2. Warum gilt der satz des pythagoras.

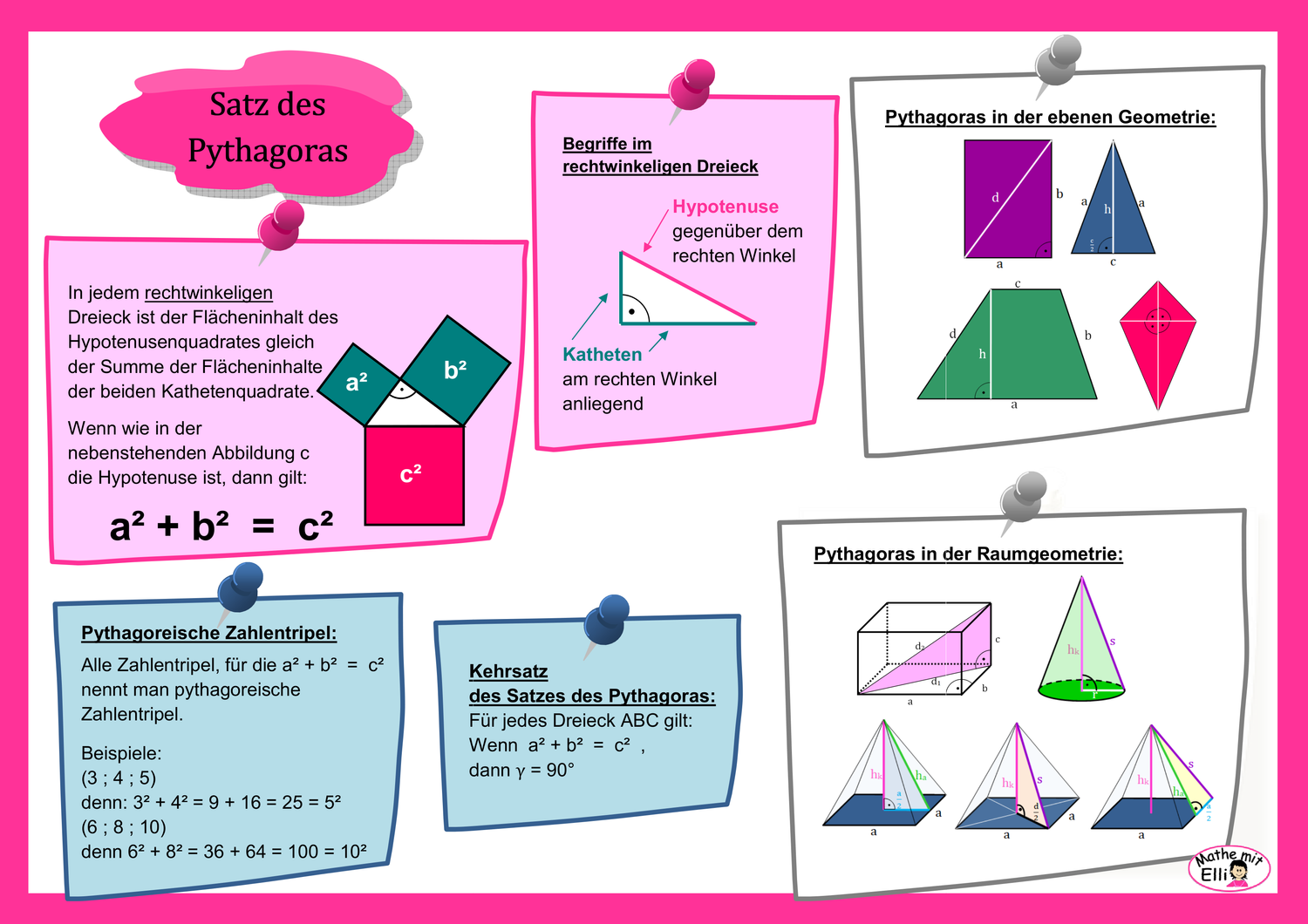
Sie werden als pythagoreisches tripel bezeichnet. Hat dieser dreieck einen rechten winkel. A 4 cm b 3 cm gesucht. Seitenlänge c in cm.

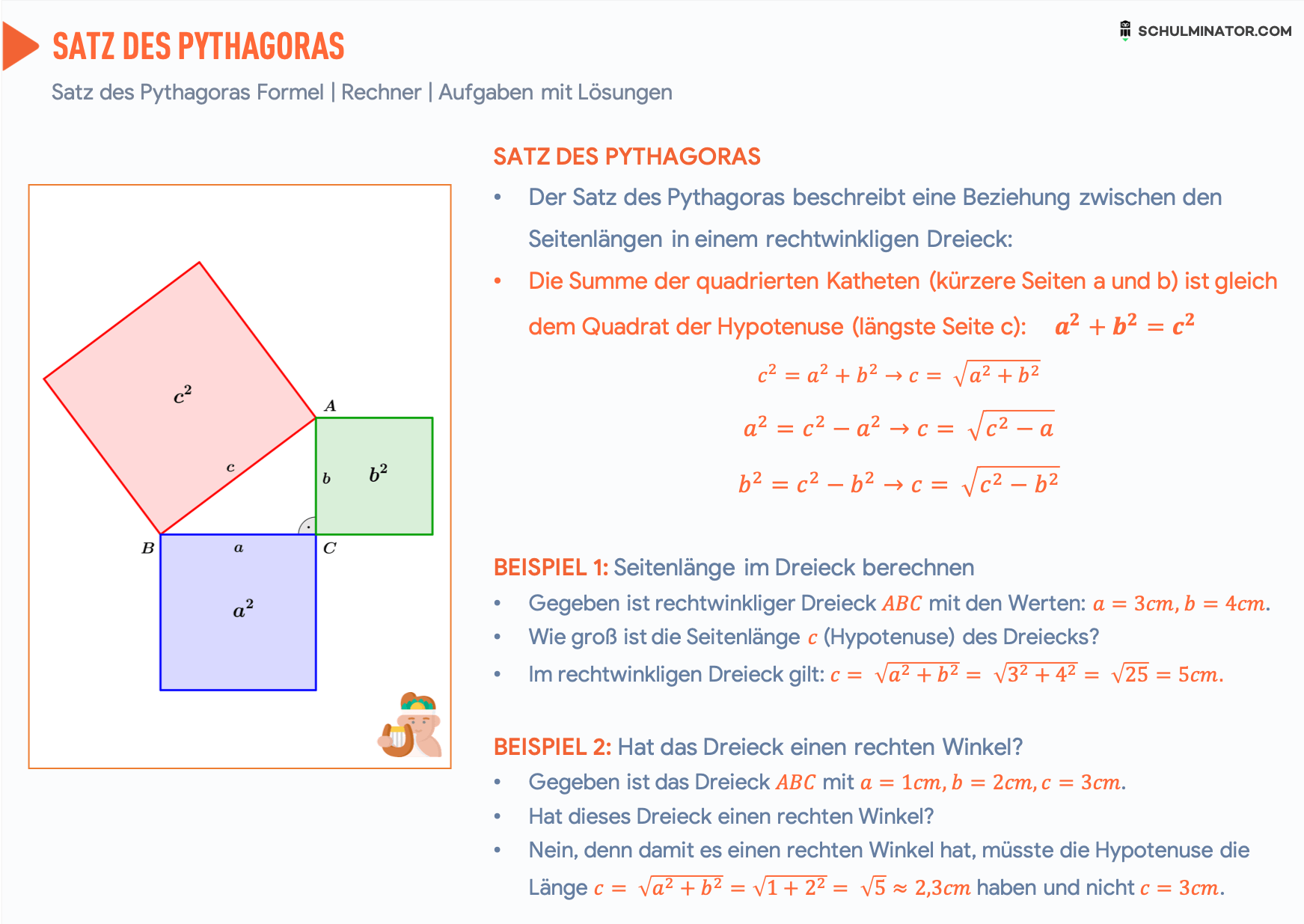
Daraus ergibt sich auch die formel a 2 b 2 c 2. Man kann sich den satz des pythagoras auch grafisch vorstellen. A 2 b 2 c 2. B 2 144.

Hat das dreieck einen 90 winkel. 169 c 2. C 2 26 2 676. Kostenlose mathe fragen teilen helfen plattform für schüler studenten mehr infos im video.

übungsbeispiele zum satz des pythagoras 1 berechne die fehlenden seiten eines rechtwinkligen dreiecks mit der hypotenuse c und den katheten a und b. Nun setzt man die gegebenen werte ein. 81 b 2 225. Es kommt das gleiche raus.

A 2 a2 und der fläche. Dazu erweitert man jede seite vom dreieck zu einem quadrat. Was hat das mit einem rechten winkel zu tun. Wie geht man vor.

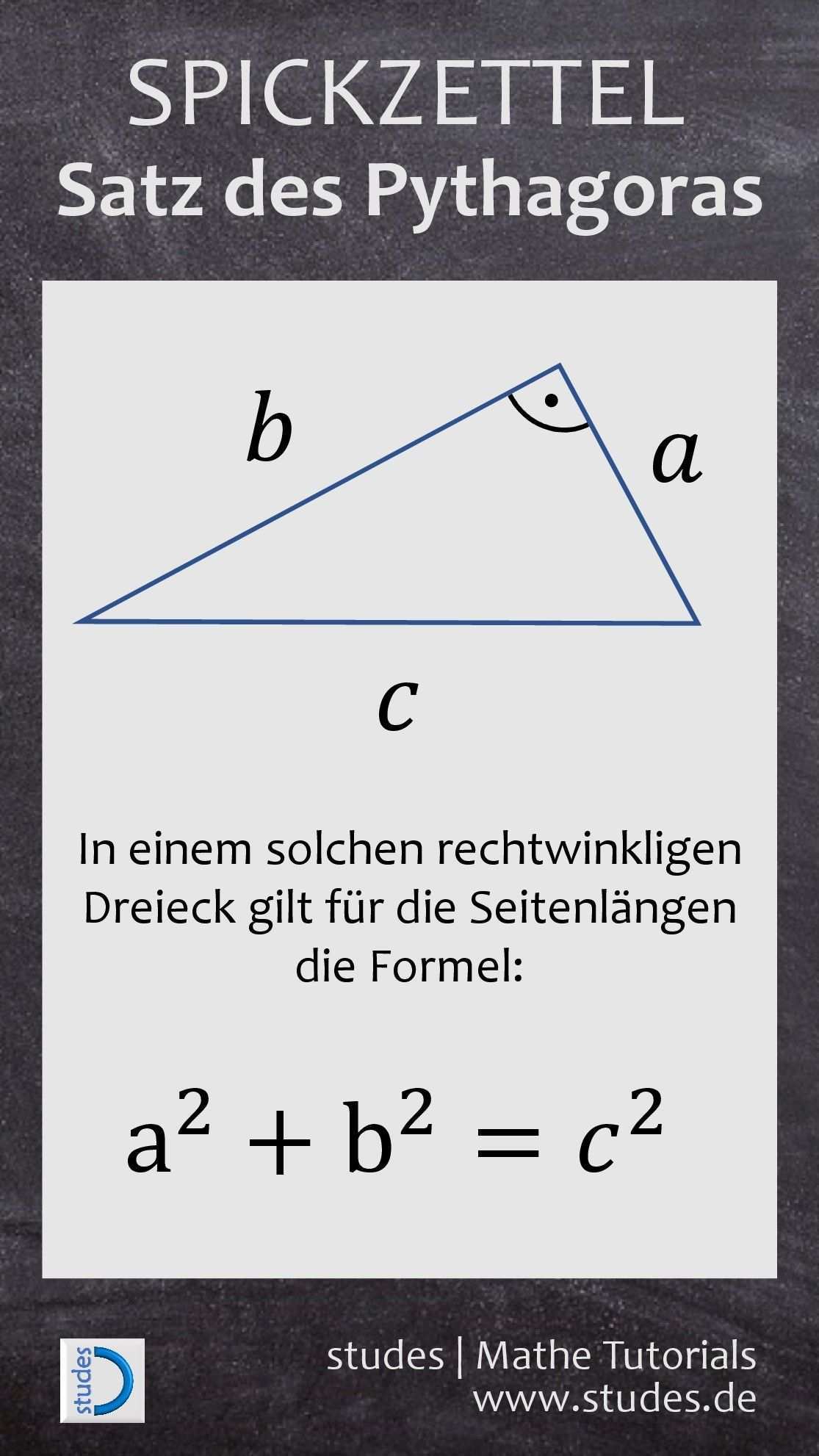
Wie lautet die formel. C c sind in diesem dreieck die katheten damit ergibt sich nach dem satz des pythagoras folgende formel. Drei natürliche zahlen die wie im ersten beispiel den satz des pythagoras erfüllen gelten in der mathematik als besonders. Du kannst die gesuchte länge mit dem satz des pythagoras finden.

Nachdem man die 81 von beiden seiten abzieht. C 4 mathrm cm c 4cm. Deshalb darfst du den satz des pythagoras anwenden. A 2 b 2 c 2.

Ja zwischen den seiten a und b. Eine leiter wird an eine mauer gelehnt. Was muss man wissen. A 2 b 2 c 2.

Aufgaben satz des pythagoras. Historische funde belegen dass menschen bereits vor jahrtausenden die bedeutung solcher tripel kannten. Geometrischer beweis des satzes des pythagoras animation eine algebraische lösung ergibt sich aus dem linken bild. 9 2 b 2 15 2.

Was kann man damit machen. Im zweiten beispiel haben wir eine textaufgabe sachaufgabe zum satz des pythagoras. A b c das ist der satz des pythagoras. Wie kann man ihn beweisen.

Textaufgabe satz des pythagoras. B 2 b2 also. 5 2 12 2 c 2. Die leiter wird so angelehnt dass sie 20 cm unter dem oberen mauerrand entfernt anliegt.

25 144 c 2. C 4 c m. Die leiter ist dabei so lange wie die mauer hoch. C 2 c2 entspricht also der summe der fläche.

Die fläche vom roten quadrat plus der fläche vom grünen quadrat ist so groß wie die fläche vom blauen quadrat. B 3 mathrm cm b 3cm und. A 2 b 2 c 2.