Rechtwinkliges Dreieck Beispiel

Cos β q a a c.
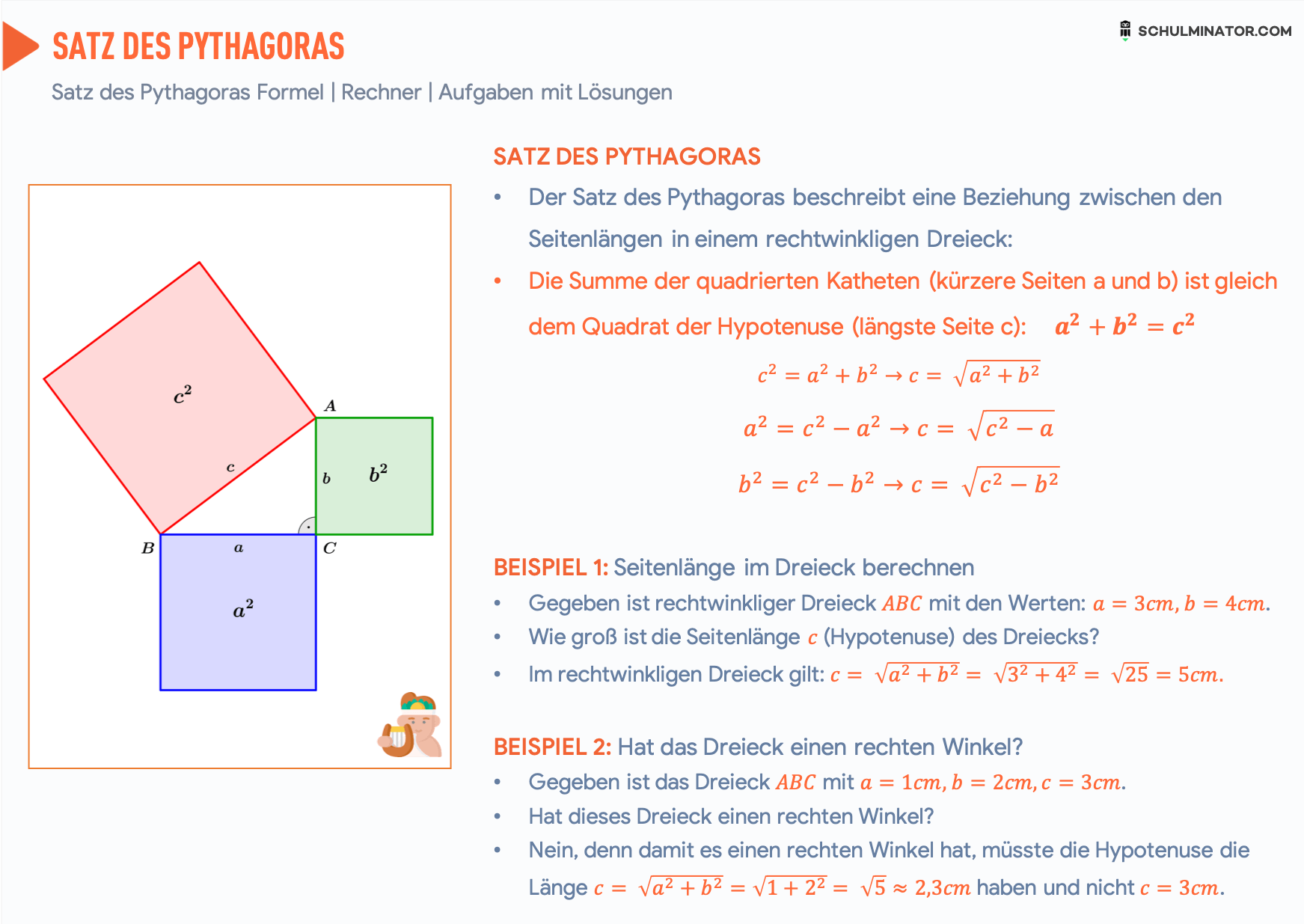
Rechtwinkliges dreieck beispiel. Ein rechtwinkliges dreieck ist meist durch zwei größen zusammen mit dem rechten winkel eindeutig bestimmt. Eine erklärung was ein rechtwinkliges dreieck ist und wie man mit dem satz des pythagoras an diesem rechnet. Liegen a b und c auf einem kreis und geht ab durch den mittelpunkt so ist das dreieck abc bei c rechtwinklig. Tan α h p a b.
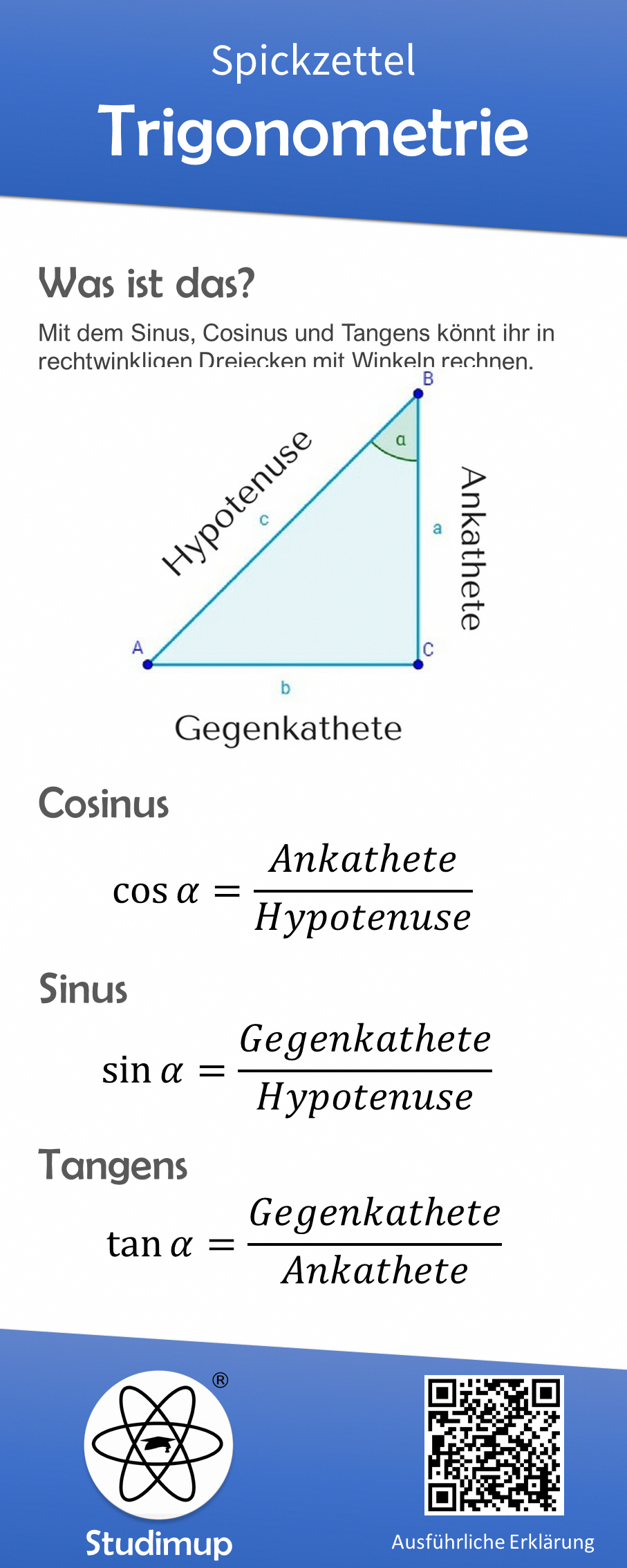
Für jedes rechtwinklige dreieck gilt. Sin α cos β cos α sin β tan α 1 tan β weitere zusammenhänge und formeln in den protokollen des rechenwegs. Der flächeninhalt eines rechtwinkligen dreiecks ist halb so groß wie der flächeninhalt des rechtecks. Sin β h a b c.
Die summe der winkel ist 180 es gilt. Flächeninhalt und umfang des rechtwinkligen dreiecks das rechtwinklige dreieck besteht aus senkrechten katheten und der hypotenuse längste seite. Als hypotenuse bezeichnet man die längste seite eines rechtwinkligen dreiecks. Die hypotenuse c beträgt 10 63 cm.
Hypotenusenabschnitte p und q. Cos α p b b c. Man spricht vom thaleskreis über ab. Sie liegt dem rechten winkel gegenüber.
Das programm erlaubt es aus den folgenden größen zwei auszuwählen und ihre werte einzugeben. H c ist die einzige höhe im rechtwinkligen dreieck die mit keiner seite zusammenfällt. Zeichnet man die diagonale des rechtecks ein so erhält man zwei deckungsgleiche rechtwinklige dreiecke. Winkel α und β.
Die länge der seiten kann man anhand des satzes des pythagoras festlegen die größe der winkel anhand goniometrischer funktionen. Diese sätze wiederum lassen sich zur berechnung von anderen schwierigeren figuren verwenden. Die katheten sind also die beiden seiten des rechtwinkligen. In der abbildung gilt.
A 8 cm b 7 cm. Sie stehen senkrecht zueinander und bilden den rechten winkel. Tan β h q b a. Das rechnen am rechtwinkligen dreieck wird in diesem artikel behandelt.
Ist das dreieck abc bei c rechtwinklig so liegt c auf dem thaleskreis über ab. In einem rechtwinkligen dreieck stimmen die höhen auf die katheten mit den katheten überein. Rechtwinklige dreiecke sind etwas besonderes denn an ihnen definiert man viele sätze wie zum beispiel den satz des pythagoras oder den satz des thales. Folgende inhalte werden angeboten.
Berechne die hypotenuse c. C a b c 8 7 c 10 63 cm. H a b und h b a die höhe auf die hypotenuse in der abbildung. Aufgaben übungen bzw.
Als kathete wird jede der beiden kürzeren seiten in einem rechtwinkligen dreieck bezeichnet. Beispiele mit zahlen und einheiten welche die berechnungen am rechtwinkligen dreieck zeigen. Katheten a und b. α β 90.