Mittelwertsatz Der Integralrechnung Beispiel

Der mittelwertsatz gilt nicht wenn die funktion irgendwo zwischen und und sei es nur in einem einzigen punkt nicht differenzierbar oder gar nicht definiert ist.

Mittelwertsatz der integralrechnung beispiel. Satz 15vj mittelwertsatz der integralrechnung sei f f f eine auf dem intervall a b a b a b stetige funktion. Für stetige funktionen ergibt sich wenn wir s inf x a b f x und s sup x a b f x setzen die zweite version des mittelwertsatzes bringt eine nichtnegative sog. Berechnung des mittelwertes in der integralrechnung. 7 1 4 an den stellen und so gilt.

A b r displaystyle f g colon a b to mathbb r funktionen f displaystyle f monoton und g displaystyle g stetig. Min f a b b a p x dx b a f x p x dx max f a b b. A b r ein ξ a b gibt sodass rb a f x dx f ξ b a. Sei f a b r stetig p a b r integrierbar und p x 0f ur a x b.

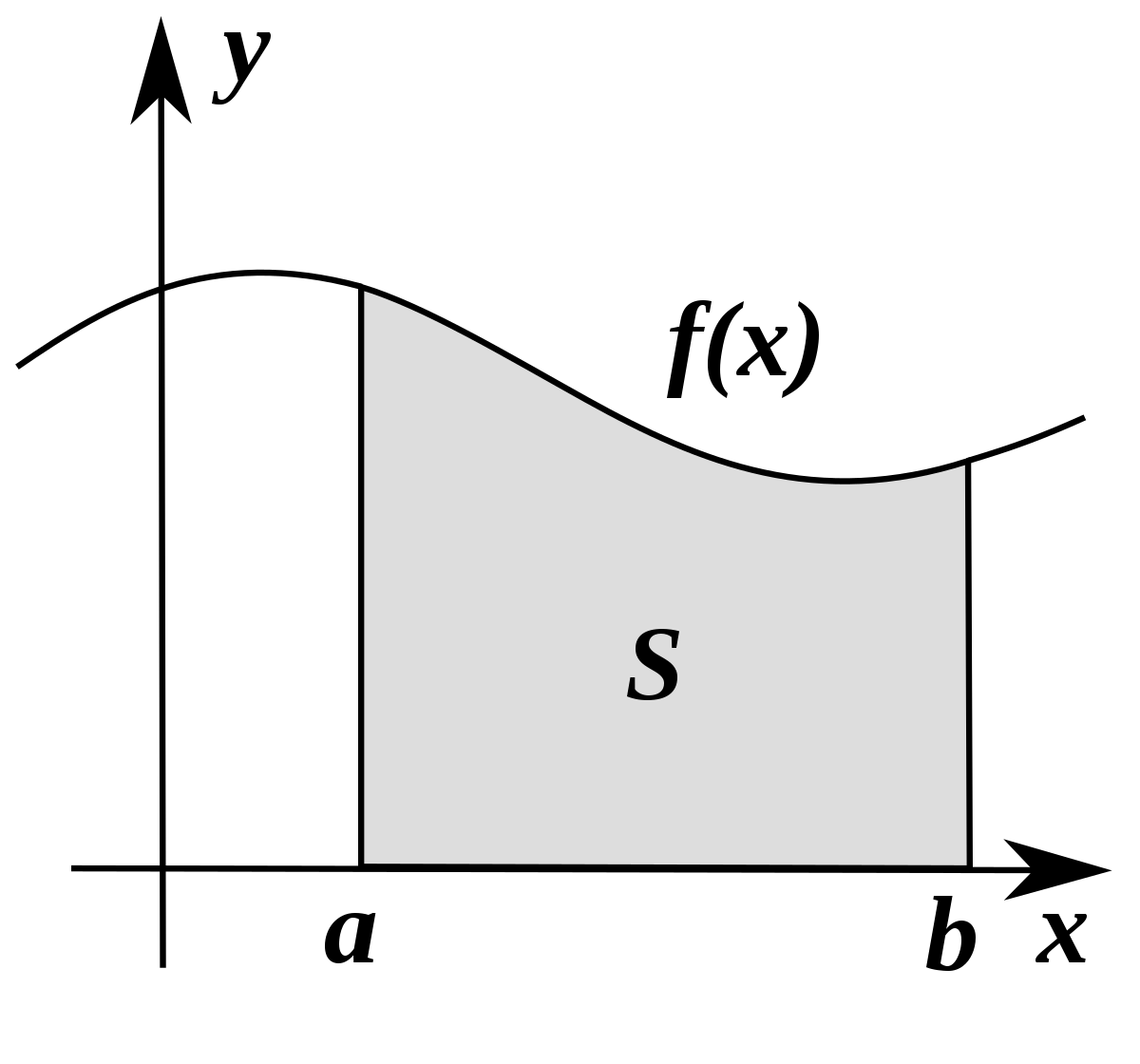
Der zusatz für funktionen deren wertebereich ein intervall ist wie z. Geometrisch lässt sich dieser erste mittelwertsatz der integralrechnung so interpretieren dass zu jedem flächeninhalt den mit der x achse einschließt ein entsprechendes rechteck mit derselben fläche gefunden werden kann. Zweiter mittelwertsatz der integralrechnung seien f g. Reelle analysis integration der mittelwertsatz der integralrechnung.

Dann existiert ein ξ a b displaystyle xi in a b so dass. Satz sei f eine stetige funktion in a. Der mittelwert von auf dem intervall berechnet sich als der mittelwert einer funktion soll häufig im kontext von anwendungsbezogenen aufgaben berechnet werden. Eine mögliche formulierung einer solchen aufgabe findest du im folgenden beispiel.

Nicht verwechseln mit der durchschnittlichen änderungsrate analysis. Letztere eigenschaft ist offensichtlich zu. B mit geometrische interpretation es gibt mindestens ein ξ aus a. Die stelle ξ ist im allgemeinen nicht der mittelwert von a und b.

Visualisierung zum mittelwertsatz der integralrechnung. Dann gibt es mindestens eine stelle ξ in a. Betrachtet man die funktion siehe abb. Dann gibt es ein x 0 a b x 0 in a b x 0 a b mit.

Da f x stetig und p x 0folgt. Dann existiert ein ξ a b mit b a f x p x dx f ξ b a p x dx. Ein auto beschleunigt 30 sekunden lang.