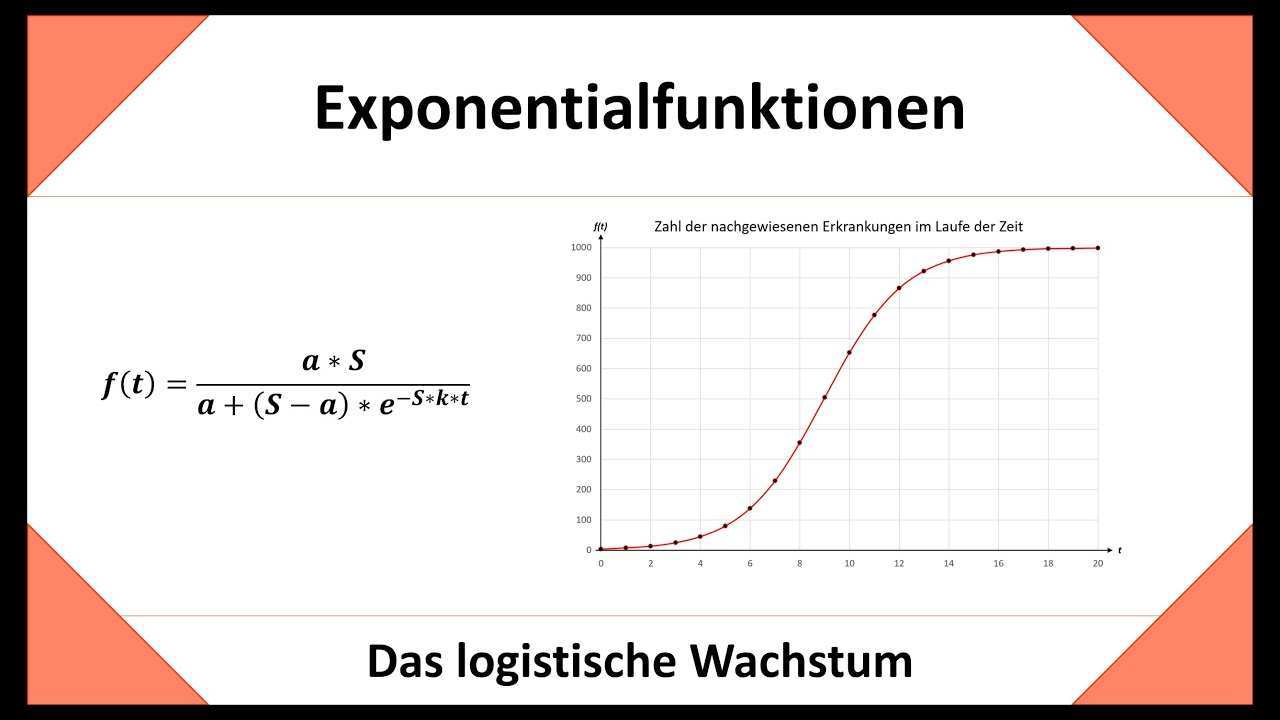
Logistisches Wachstum Beispiel

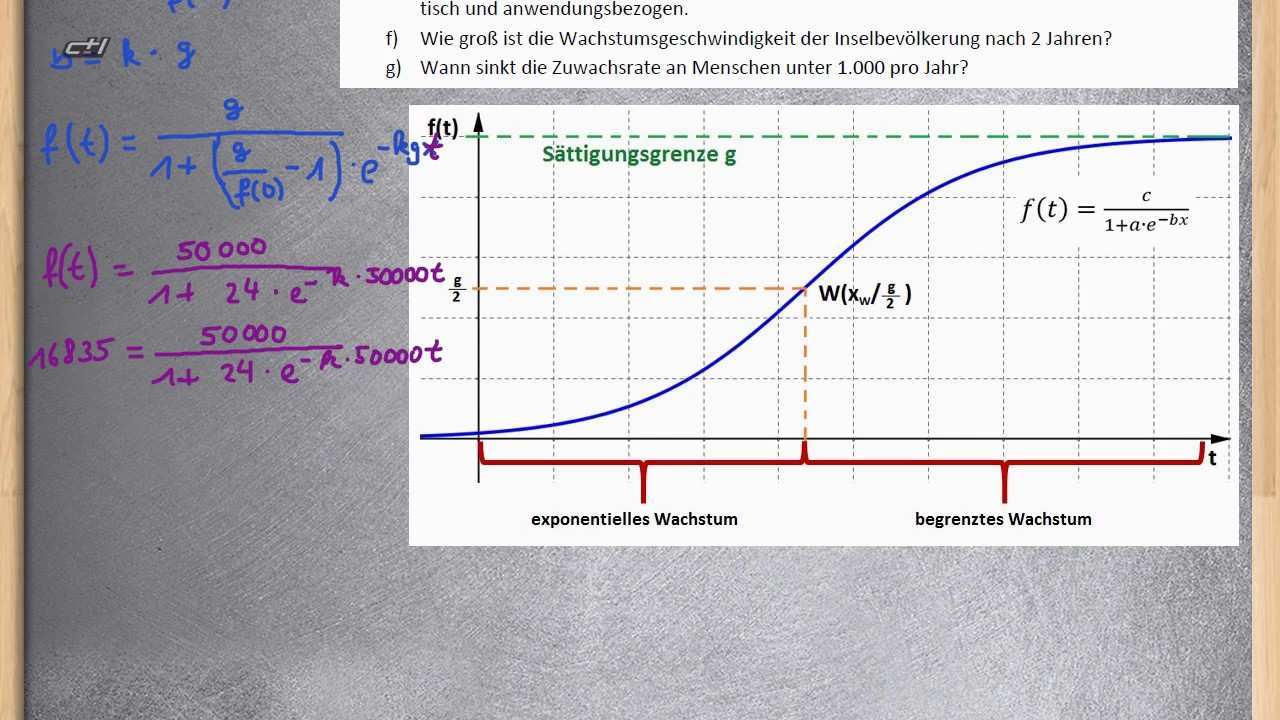
Diskretes modell rekursiv f n 1 f n 0 6 40 000 f n mit f 0 20 000 nach 5 stunden a logistisches wachstum kontinuierliches modell explizite darstellung die population wächst im gesamten zeitraum.

Logistisches wachstum beispiel. Zunächst wächst sie annähernd exponen. Werde einser schüler und klick hier https www thesimpleclub de goin diesem video geht s um folgende punkte logistisches wachstum am beispiel hasen graph. Beispiele für populationen sind die anzahl an bakterien in einem behälter oder der stand deines bankkontos. Eine variable die ein logistisches wachstum durchmacht wächst zunächst exponentiell.

Auch hier kann man sich mit viel phantasie eine logistische wachstumskurve denken. Vergleicht man das lineare wachstum mit dem logistischen wachstum sieht man. Logistisches wachstum als alternatives modell zu exponentiellem wachstum wie im beispiel der schachbrettlegende wächst unbegrenzt exponentielles wachstum schließlich dramatisch schnell an es geht sehr schnell ins quasi unendliche. Dies ist das berühmte beispiel der schafe in tasmanien.

Eine logistische funktion stellt ein wachstum da welches exponentiell ansteigt und durch wachstumshemmende faktoren zu einer sättigung führt. Die zahlen auf der y achse bedeuten millionen. Nach einiger zeit nimmt die wachstumsrate ab und die funktion nimmt ab wodurch eine sigmoidale oder s förmige kurve entsteht. In der wirklichkeit ist exponentielles wachstum aber nur theoretisch unbegrenzt es geht praktisch.

Logistisches wachstum einfach erklärt bei einem wachstumsprozess betrachtest du das verhalten einer bestimmten kenngröße oft population genannt im verlauf der zeit. Lösung a kontinuierliches logistisches wachstum. Dabei ist t die zeit in jahren und h t die höhe in dezimetern. Begrenztes wachstum mit g 40 000 f 0 20 000 und q 0 60.

Logistisches wachstum am beispiel einer hefekultur katharina reichert 6 2 1 3 logistisches wachstum. Höhenwachstum eines strauches das höhenwachstum eines strauches wird in guter näherung durch eine logistische funktion beschrieben. Aufgabenstellung gib zu p 0 p 0 40 und p 1 80 mit der obergrenze k 1000 a die funktionsgleichung für kontinuierliches logistisches wachstum b die rekursive darstellung für diskretes logistisches wachstum an.