Kurvenintegral Berechnen Beispiel

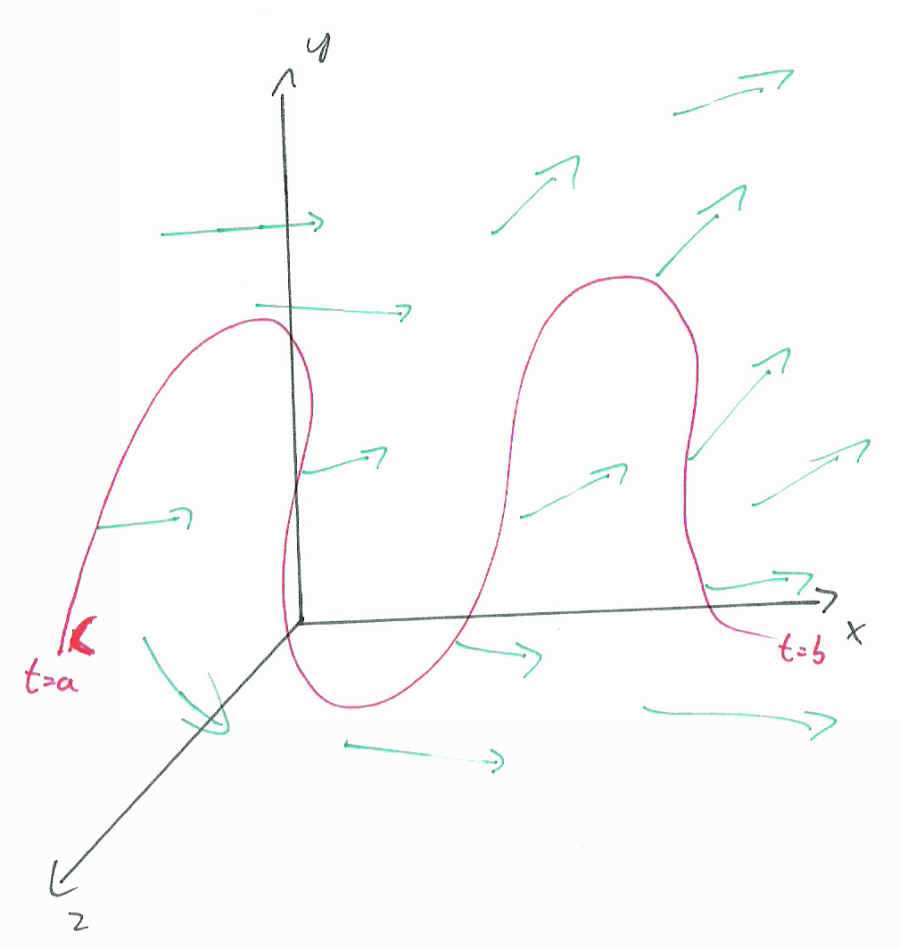
Man sollte das kurvenintegral über dem vektorfeld f x y 2xy x x y t entlang des weges ω t t t t von punkt a nach punkt b berechnet werden siehe zeichnung.

Kurvenintegral berechnen beispiel. Zu berechnen wir eine normale determinante dabei wird die ableitung vom vektorfeld gebildet beispiel sei v 0 b xy z x y ez 1 c a dann ist rot v e e e x y z. Was zunächst kompliziert aussieht ist eine. Das eben beschriebene vorgehen mit dem man ein kurvenintegral berechnen kann soll nun an einem beispiel verdeutlicht werden. Haben wir eine stetige skalare funktion f und eine mindestens ein mal stetig differenzierbare kurve ω t in parametrisierter form gegeben so berechnet sich das kurvenintegral von f entlang der kurve ω t wie folgt.

Linienintegral der funktion entlang des kreises um den ursprung mir radius berechnen. Kurvenintegral methode wenn g einfach zusammenhängend ist und v die integrabilitätsbedingung erfüllt dann gibt es eine stammfunktion f. In diesem fall gibt f x y fur jeden punkt x y der etwa. Kostenlose mathe fragen teilen helfen plattform für schüler studenten mehr infos im video.

Felder gradient kurvenintegral 2 1 partielle difierentiation 2 1 1 funktionen mehrerer variabler eine funktion kann von mehr als einer variablen abh angen. Zum beispiel k onnte f x y das h ohenrelief eines gebirges darstellen. Beispiel wir betrachten die konstante funktion f x y h f x y h f x y h und wollen für diese das kurvenintegral über den kreis mit dem radius r r r um die ursprung berechnen. Das vektorfeld f x 2xy z3 x2 3z 3xz2 3y besitzt das potential ϕ x x2y xz3 3yz.

F xy 2 xy x 11 x6 f x x5 f x 5x4 w3 c 3 fx fy f x dx 0 1 x11 5 x10 dx 1 12 5 11 w 1 c 1 f d r 0 583 w 2 c 2 f d r 0 567 w1 w2 w3 71 132. Der kreis hat die parameterdarstellung x r cos t x r cdot cos t x r cos t und y r sin t y r cdot sin t y r sin t formel 15vs. Die integrationsgrenzen können einfach aus der zeichnung abgelesen. Zum besseren verständnis rechnen wir ein beispiel mit einem zweidimensionalen vektorfeld durch.

F ur eine c1 kurve c t von p 1 1 2 nach q 3 5 2 gilt z c f x dx ϕ q ϕ p 9 15 24 interpretiert man f x als elektrisches feld so gibt das kurvenintegral zweiter art die spannung zwischen den beiden punkten pund qan.