Gedaempfte Schwingung Beispiel

G xg 9810mm 10mm s 31 32 1 s d 1 d 2 31 32 1 s 1 0 022 31 31 1 s c 2m 981 1 s2 1000kg 981 n mm.

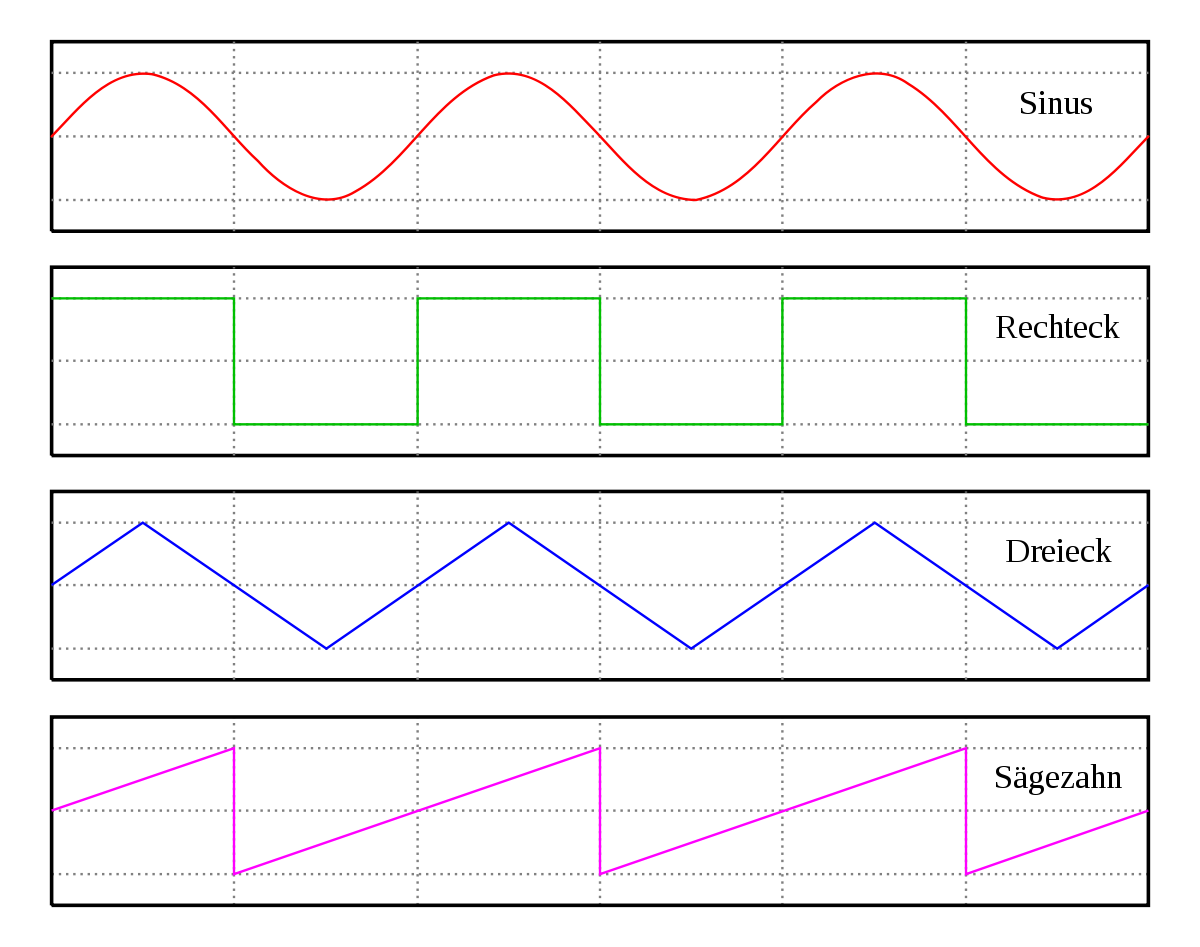
Gedaempfte schwingung beispiel. Sonderfall delta 0. Auslenkung x rückstellkraft der feder c losgelassen. Die auslenkung zu einem zeitpunkt gibt den momentanen die amplitude den maximal möglichen wert der größe an. Als harmonisch wird eine schwingung bezeichnet deren verlauf durch eine sinusfunktion beschrieben werden kann.

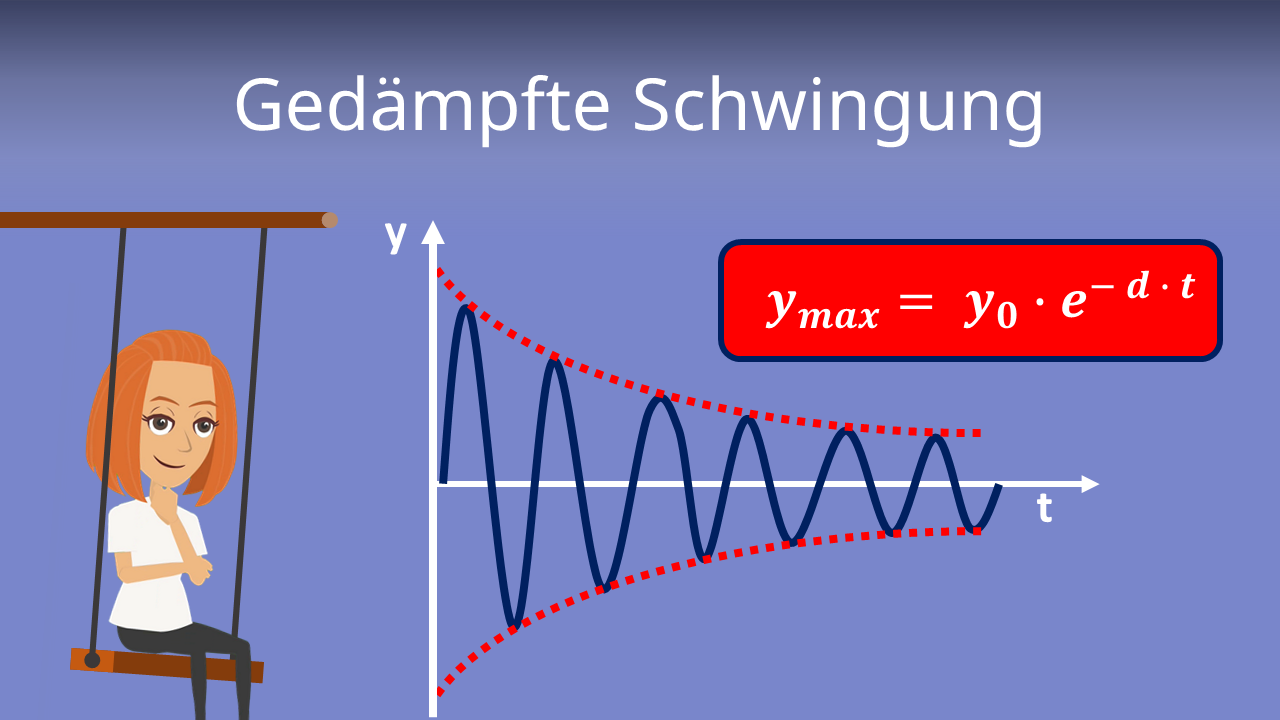
Als dämpfung wirkt dabei die stokes sche reibungskraft durch die zähigkeit η der flüssigkeit mit einer reibungskraft f st 6 π η r υ laminare reibung. Bei der gedämpften schwingung ist die amplitude a über die zeit nicht mehr konstant sondern ändert sich aufgrund von reibung. Um die auslenkung einer gedämpften schwingung in abhängigkeit von der zeit zu beschreiben muss man nun in der schwingungsgleichung für harmonische schwingungen die amplitude durch den ausdruck ersetzen denn diese ist ja bei gedämpften schwingungen nicht konstant sondern sie wird kleiner. Räumlich und zeitlich wiederkehrender periodischer vorgang zu besprechen.

Ungedämpfte freie schwingung gedämpfte freie schwingung erzwungene gedämpfte schwingung fr dx ma dx ungedämpfte freie schwingungen beispiel federpendel a in ruhe b gespannt. Diese gibt an wie stark die schwingung gedämpft ist. Ist eine reibungskraft gegeben die abhängig von der geschwindigkeit v ist z b. Die periodendauer oder die schwingungsdauer ist die zeit die.

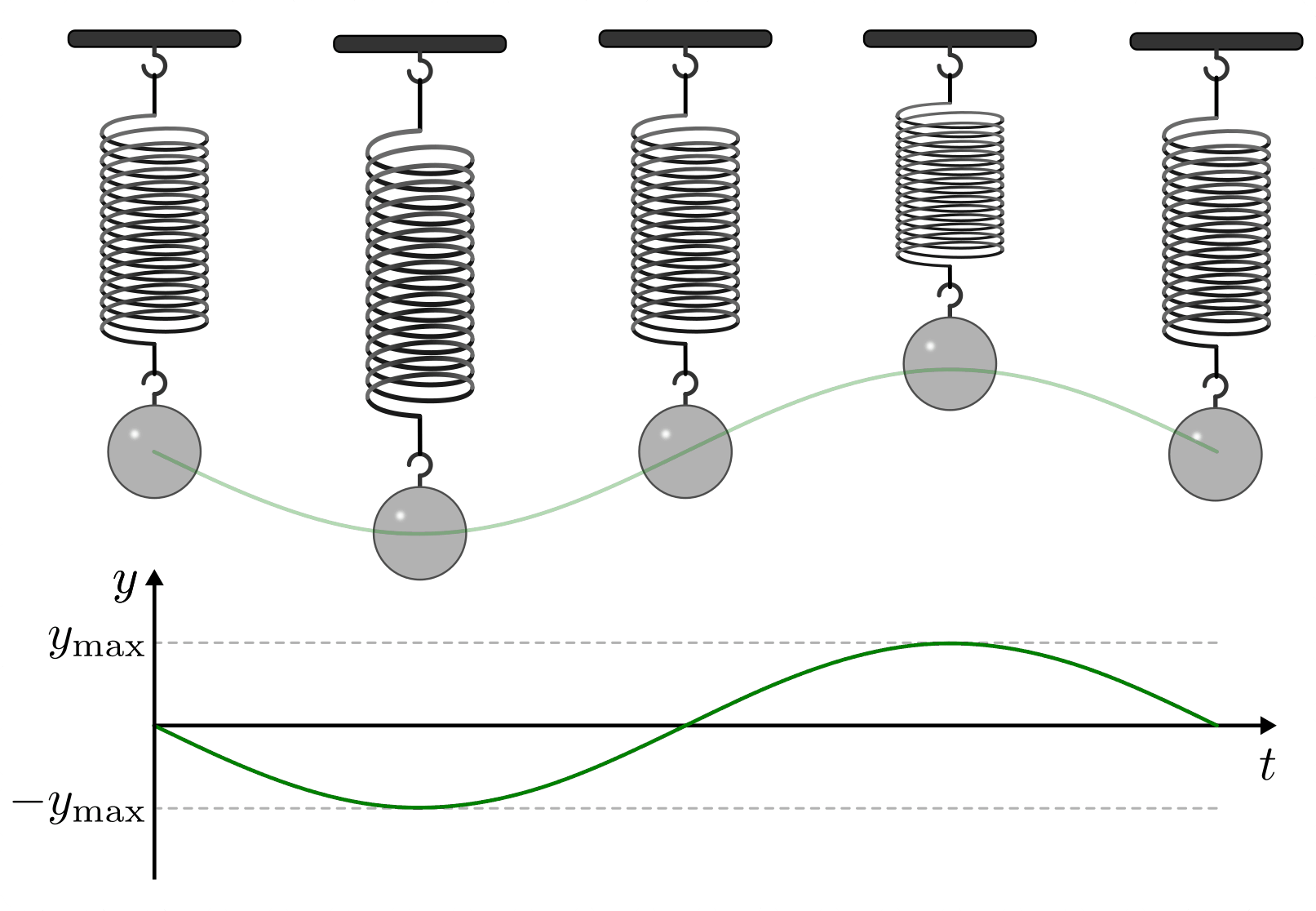
Wir wollen nun den bewegungsablauf einer gedämpften schwingung am beispiel einer kugel in öl untersuchen. S 0 2 m f frac 1 5 hz und phi 0 0 und delta 0 1 lade animation. Die schwingung ist ungedämpft harmonisch. Die gedämpfte schwingung aufgrund von reibung lässt sich mit der sogenannten dämpfungskonstante delta beschreiben.

Die durch die reibung entstehende dämpfung wird mit der dämpfungskonstante und der abklingkonstante in einer schwingungsgleichung mathematisch beschrieben.