Gausssches Eliminationsverfahren Beispiel

Das gaußsche eliminationsverfahren oder gauß verfahren nach carl friedrich gauß ist eine standardmethode zum lösen von linearen gleichungssystemen lgs.
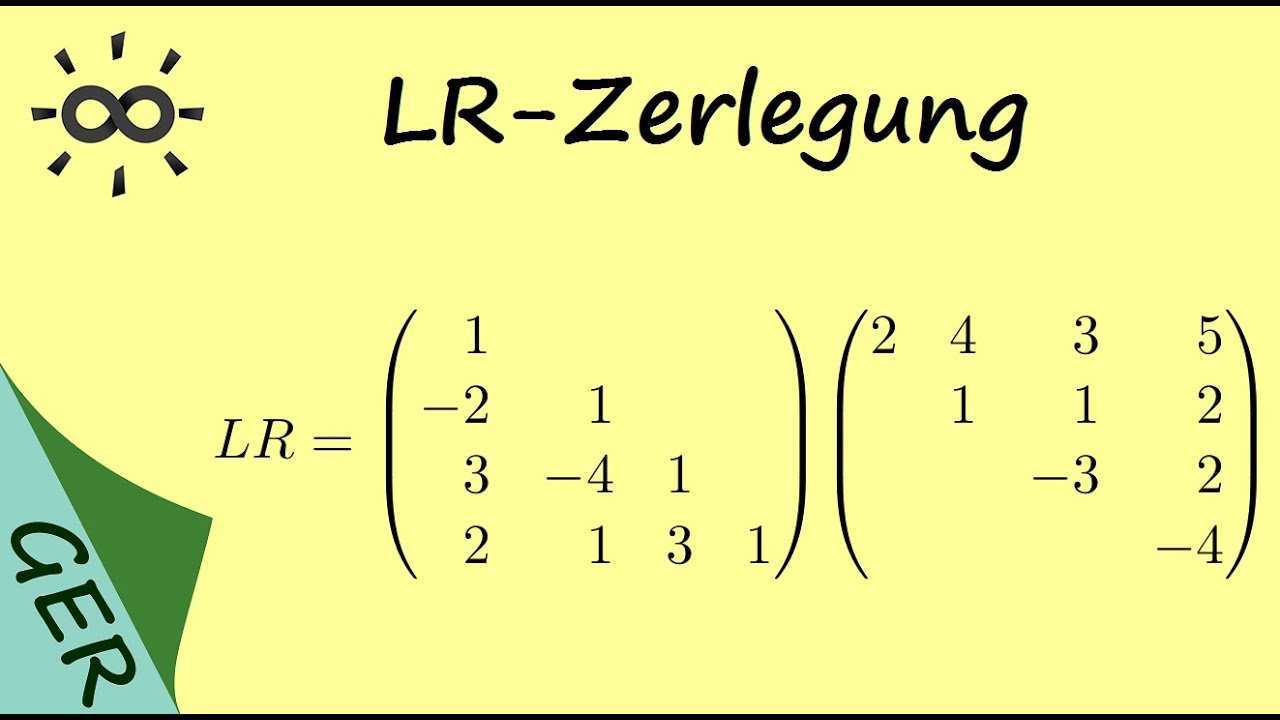
Gausssches eliminationsverfahren beispiel. Damit haben wir in diesem beispiel die lr zerlegung a lr mit l 1 0 0 0 1 1 0 0 3 10 3 1 0 2 2 3 2 1 r 1 1 3 5 0 0 3 1 0 0 0 14 3 0 0 0 0. Gauß algorithmus gauß verfahren lineare gleichungssysteme lösen gaußsches eliminationsverfahren duration. 6 1 2 3 1 3 1 1 4 2 4 1 2 3 1 2 underset. Kostenlos über 1 000 aufgaben mit ausführlichen lösungswegen.
Dann dividiert man die erste zeile durch 3 die zweite durch 4 und die dritte durch 6. Dabei wird das zu lösende gleichungssystem durch äquivalenzumformungen vgl. Bisher haben wir nur den fall behandelt dass das gaußsche eliminationsverfahren ohne zeilenvertauschungen auskommt im allgemeinen fall muss es keine lr zerlegung. Durch vertauschen von gleichungen auf stufenform gebracht.
Anschließend kann schrittweise von unten nach oben nach den. Mathematik und statistik übungsaufgaben mit lösungsweg zum thema lineare algebra lineare gleichungssysteme gauß sches eliminationsverfahren. Das gaußsche eliminationsverfahren ist ein algorithmus aus den mathematischen teilgebieten der linearen algebra und der numerik es ist ein wichtiges verfahren zum lösen von linearen gleichungssystemen das verfahren wurde um 1850 von carl friedrich gauß bei arbeiten auf dem gebiet der linearen gleichungssysteme entwickelt allerdings hatte der chinesische mathematiker liu hui bereits im jahr. Gaußsches eliminationsverfahren translation in german english reverso dictionary see also gau galosche gamasche gänschen examples definition conjugation.
Mathe by daniel jung 533 208 views 9 29. Das gaußsche eliminationsverfahren ist im allgemeinen nicht ohne zeilenvertauschungen durchführbar. 4 i i i. Mathe by daniel jung 521 171 views 9 29.
Anschließend formst du die matrix durch zeilenumformung so um dass ihre werte unterhalb der hauptdiagonalen zu 0 werden. Gauß algorithmus gauß verfahren lineare gleichungssysteme lösen gaußsches eliminationsverfahren duration. Das gaußsche eliminationsverfahren ist ein verfahren zur lösung linearer gleichungssysteme dafür wird das gleichungssystem zunächst in matrixform ausgedrückt.