Gaussscher Integralsatz Beispiel

Analysis iii tuhh wintersemester 2007 2008 armin iske 203.

Gaussscher integralsatz beispiel. Ober ache 6 a2 inkugelradius a 2 volumen a 3 6a2 a 2 3 tetraeder mit kantenl age a. Hierbei ist v ein beliebiges volumen z b. R t acost bsint. Ein würfelvolumen oder ein kugelvolumen.

Der gauˇsche integralsatz beimoberfl achenintegral. Z g f g h f gi dx z g div f x dx i g hf nido i g fh g nido i g f g n do die zweite greensche formel folgt direkt durch vertauschen von fund g. A ist dabei die geschlossene ohne löcher fläche des betrachteten volumens. Fl acheninhalt des gebiets a das von einer ellipse c mit halbachsenl angen a b 0 berandet wird parametrisierung der randkurve.

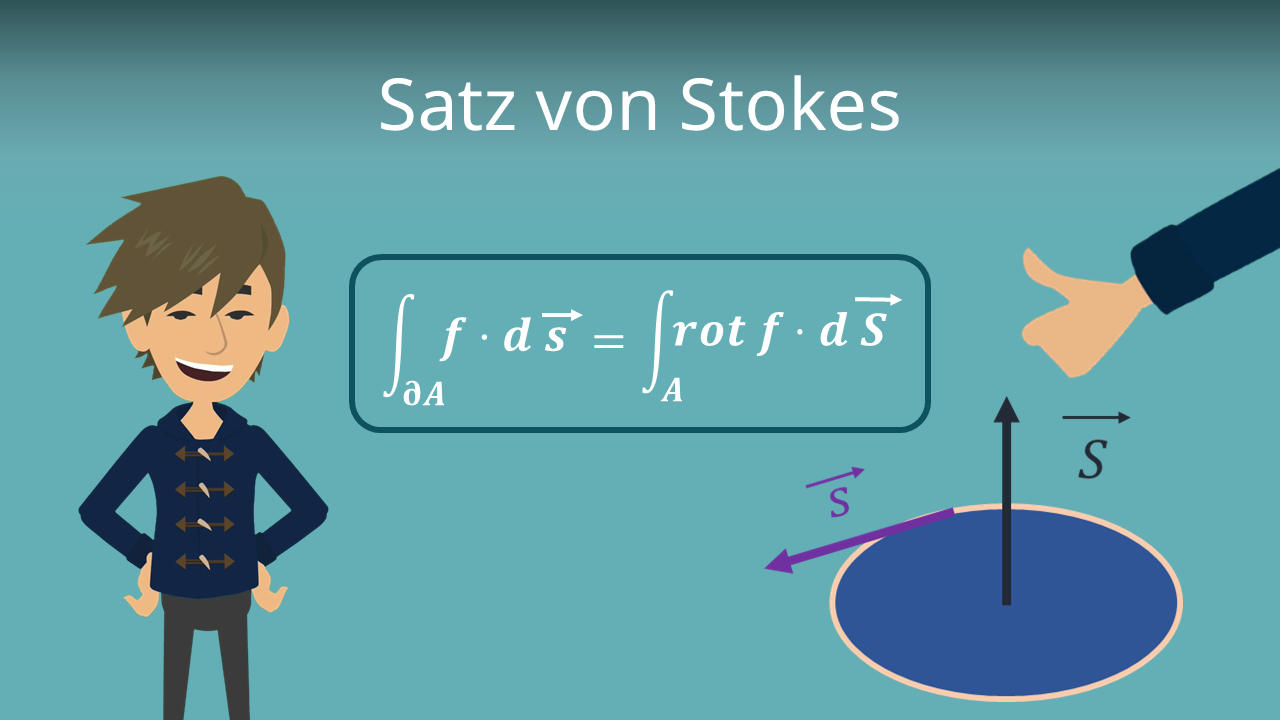
3 die integralsätze von gauß und stokes 3 1der gaußsche integralsatz 3 1definition esseig rn n n n 2 einbeschränktesgebietundk n einenatürlichezahl gheißtck glattberandet fallseszujedema geine offene umgebung u u a rn von aund eine k mal stetig differenzierbare funktionh u r gibt sodass. Wir wenden nun den gaußschen integralsatz an. T 2 0 2ˇ fl acheninhalt areaa 1 2 z c r d r 1 2 z2ˇ 0 acost bsint asint dt cost dt 1 2 ab z2ˇ 0 1dt ˇab fl achenberechnung mit dem satz von gauˇ 4 1. Beispiel polyeder v mit inkugel ber uhrt jede fl ache radius r i hesse normalform rds r z n const ds r i ds volumenberechnung mit dem satz von gauˇ 3vol v zz s rds zz s r ids r i area s hexaeder mit kantenl age a.

1 c falls es im umschlossenen gebiet l ocher gibt mussen diese bei der bestimmung des randes mitberuc ksichtigt werden. Loch definition siehe anschließendes beispiel ausgeschlossen werden.