Exponentielles Wachstum Beispiel

Alternativ können sie das wachstum auch rekursiv durch b t 1 a b t beschreiben.

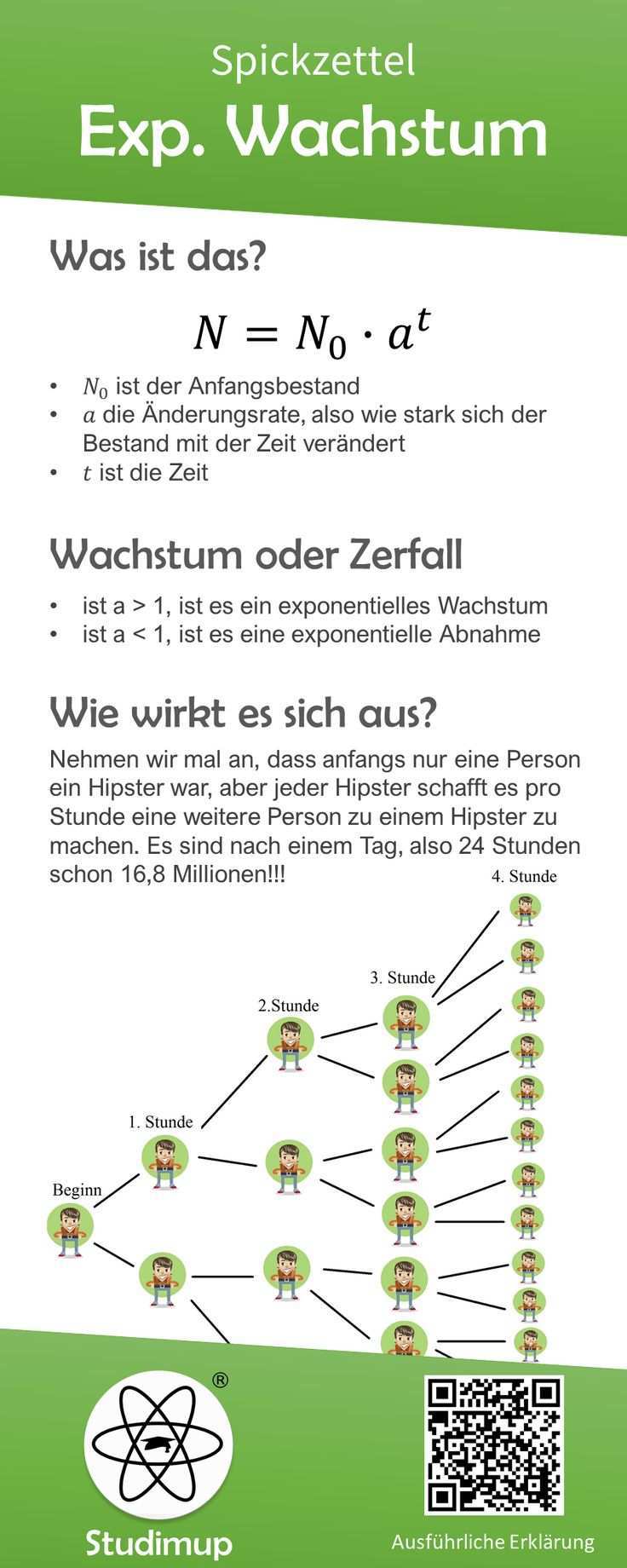
Exponentielles wachstum beispiel. Exponentielle wachstumsprozesse sind prozesse in welchen die zunahme oder abnahme immer proportional zum bestand ist sprich. Das endergebnis ist größer als der anfangswert. Im einführungsbeispiel war p 2 da immer zwei neue zombies dazukamen. B t b 0 a t.

Ein organismus wird von 500 viren befallen die sich für eine zeit lang exponentiell vermehren. N t g g n0 e λt a ist der anfangswert g die obere grenze angenommen die tierpopulation aus dem vorigen beispiel vermehrt sich nach dieser formel. Grundsätzlich gilt bei exponentiellem wachstum. Wir müssen also noch den wachstumsfaktor berechnen.

Der wachstumsfaktor ergibt sich aus der änderungsrate p p 0. Das a ist unser wachstums oder abnahmefaktor. Lässt sich die vermehrung besser durch folgende gleichung beschreiben. Der einzige unterschied ist dass etwas immer gleich viel abnimmt anstatt zunimmt.

B t beschreibt den bestand einer population zum zeitpunkt t. Es wird zunächst in einem stadtteil mit 2000 haushalten ein testverkauf begonnen. N left t right n 0 cdot 1 p t beim exponentiellen zerfall. Im hasenbeispiel wären dies also gerade die zwei hasen.

Die formel für exponentielles wachstum lautet. Unser vermögen wächst konstant um 5 pro jahr. Während jeder stunde wächst ihre anzahl um 20. Exponentielles wachstum von exponentiellem wachstum spricht man wenn eine anfangsgröße w 0 in gleichen zeitabschnitten mit einem gleichbleibenden wachstumsfaktor q vervielfacht wird der größer als 1 ist.

Nach einer woche sind 363 geräte verkauft. Zum bereits vorhandenen bestand kommt immer der gleiche prozentuale anteil dazu oder geht weg. A der verkauf der geräte soll als begrenztes wachstum modelliert werden. B 0 beschreibt dabei den bestand zum zeitpunkt t 0.

Wie groß ist die zahl der viren zu einer beliebigen zeit nach der infektion. Zu beginn im zeitpunkt 0 haben wir 1000. Bei unserem beispiel vermehren sich die bakterien also handelt es sich um ein exponentielles wachstum. Die dicke des papiers beim falten ist also ein klassisches beispiel für exponentielles wachstum.

Pro jahr bekommen wir 5 zinsen auf das kapital d. A 1 p also ist a 1 damit wird die formel für das exponentielle wachstum zu. Bezeichnen wir die dicke des papiers am anfang willkürlich mit 1 so könnte eine tabelle mit den werten für die dicke nach jedem falten folgendermaßen aussehen.