Differentialquotient Beispiel Mit Loesung

Danach erkläre ich die begriffe differenzenquotient und differentialquotient und wie man die ableitung einer funktion an der stelle x 0 bildet.

Differentialquotient beispiel mit loesung. Sf f x x 2 3 f x x2 3 im intervall. Er kann auch als die steigung der tangente an der stelle x und damit als die momentane änderungsrate interpretiert werden. Ableitung der wichtigsten funktionen. Im folgenden soll anhand einiger beispielaufgaben zum differentialquotienten die explizite berechnung des differentialquotienten mit der h methode demonstriert werden.

Sf f x x 5 3x 3 2x 2 x 7 5 f x x5 3x3 2x2 x 7 5 im intervall. In diesem fall hast du also mit dem differenzenquotient die mittlere änderungsrate zwischen. Dann wiederhole ich die potenzregel die konstantenregel und die summenregel. F x x 2 3.

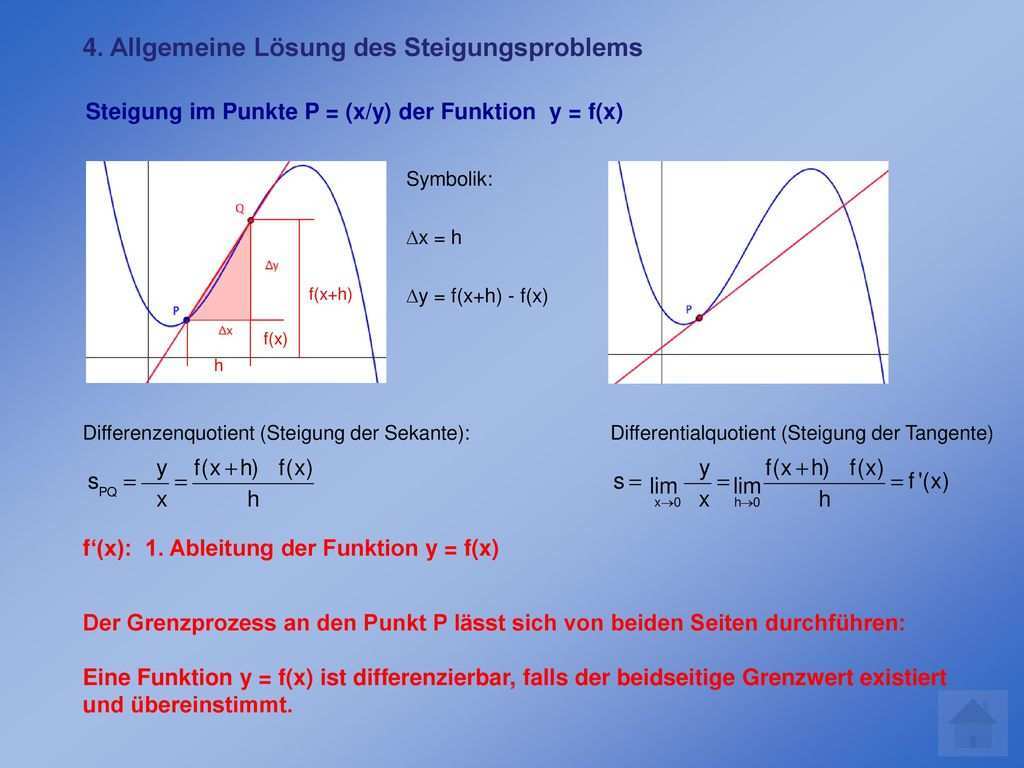
Der differentialquotient ist der grenzwert des differenzenquotienten. Die ableitung einer funktion kann über den differentialquotienten hergeleitet werden. Werde einser schüler und klick hier https www thesimpleclub de goweil auf dem differenzialquotient sehr viel aufbaut ableitungen berechnen wollen wir na. Ableitung mittlere momentane änderungsrate differenzenquotient matheaufgaben rechnerische und graphische bestimmung von mittlerer und lokaler änderungsrate.

Zum beispiel kann man die steigungen auf einer straße berechnen. Hierzu stelle ich mehrere beispiele vor. Zusammenhang zwischen f und f anhand von graphen lehrplan baden württemberg gymnasium 9. Für die geschwindigkeit rechnest du nun strecke durch zeit.

Differentialquotient lim x1 x0 f x1 f x0 x1 x0 differenzenquotient lim x 1 x 0 f x 1 f x 0 x 1 x 0. Untersuchung von abschnittsweise definierten funktionen und betragsfunktion auf differenzierbarkeit. Interaktive aufgaben und übungen mit lösungen und erklärungen zum thema differentialquotient momentane änderungsrate momentane steigung. 3 sf 0 3 0 3 lösung anzeigen.

Das heißt du berechnest die steigung der sekante also das eingezeichnete steigungsdreieck aus nämlich.