Chi Quadrat Beispiel

Man unterscheidet vor allem die folgenden tests.

Chi quadrat beispiel. Beispiele und aufgaben zum chi quadrat anpassungstest a beispiele zum anpassungstest. Ein chi quadrat unabhängigkeitstest kann angewandt werden wenn man zwei nominalskalierte variablen hat und prüfen möchte ob die zwei variablen unabhängig sind oder ob ein zusammenhang besteht. Wir haben ein approximatives ergebnis von 63 06. Hier wird geprüft ob zwei merkmale.

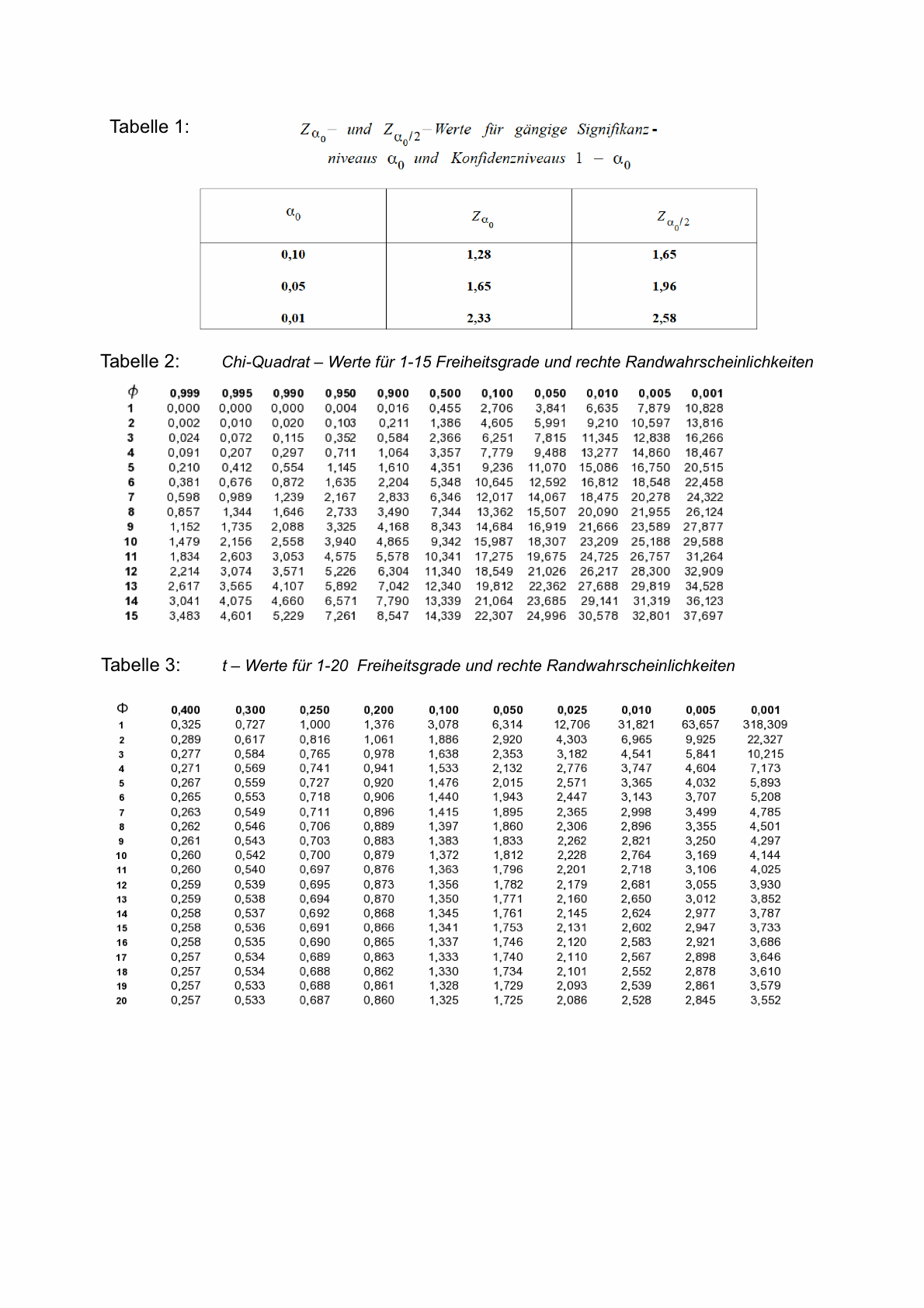
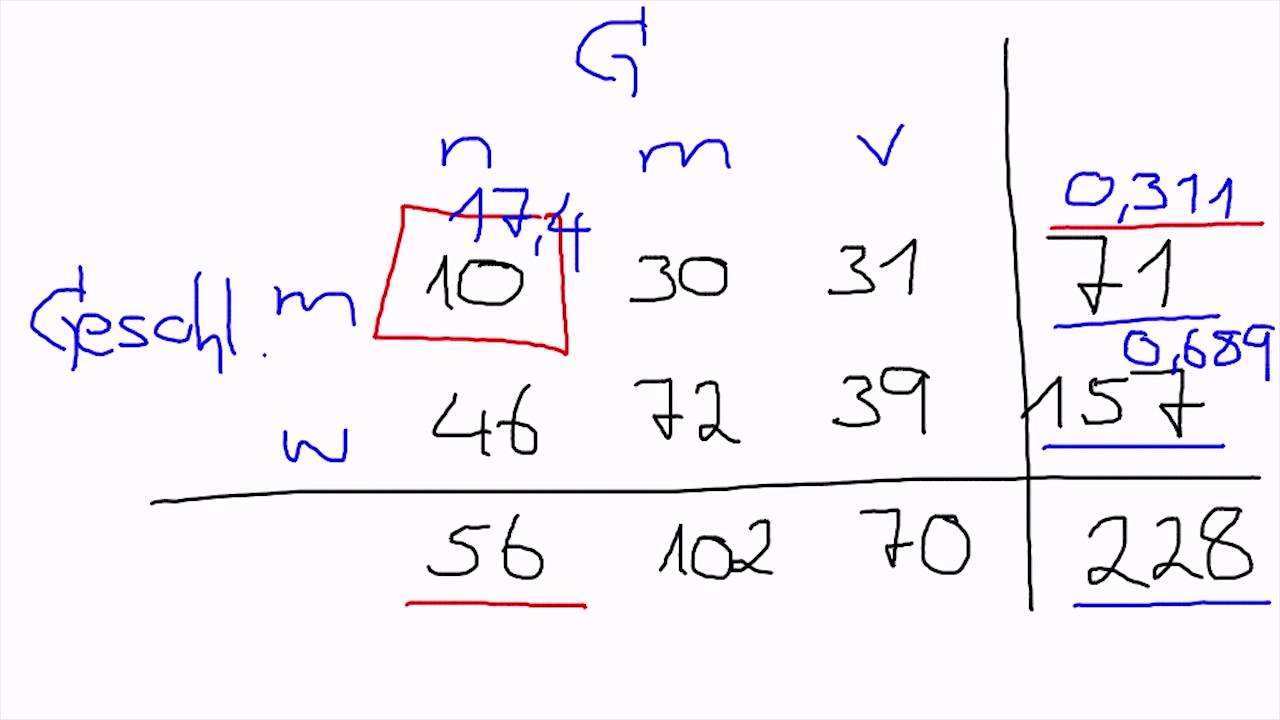
Das signifikanzniveau legst du für eine berechnung dieser art ganz einfach auf 5 fest. Für beispiel 1 den zusammenhang zwischen geschlecht und dem spielen eines instruments hast du einen chi quadrat wert von 12 81 berechnet. Verteilungstest auch anpassungstest genannt. Zuerst suchen wir uns den wert des quantils in der verteilungstabelle der standardnormalverteilung.

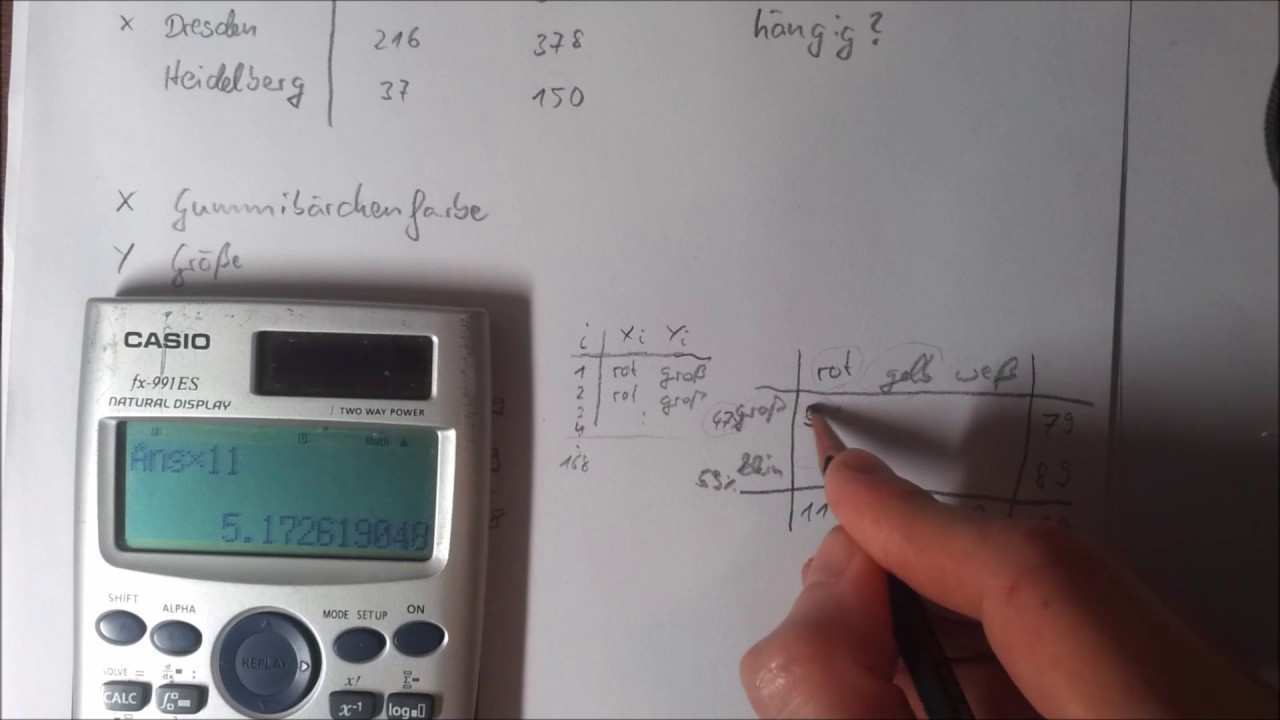
Um diese hypothese zu testen zeichnet ein unabhängiger forscher die anzahl der kunden auf die in einer bestimmten woche in den shop kommen und stellt folgendes fest. Besteht zwischen dem geschlecht des autohalters nominalskalierte variable 1 und der farbe des. Jetzt setzen wir dieses zwischenergebnis und unser n in die formel ein und erhalten. Damit sollten wir nun alle fragen geklärt haben.

Chi quadrat verteilung beispiel. Dazu befragen wir insgesamt 250 personen von drei verschiedenen studienrichtungen nämlich jura naturwissenschaften nw und sozialwissenschaften sw und erhalten folgende antworten. Eine beispielhafte fragestellung lautet. Mit chi quadrat test test bezeichnet man in der mathematischen statistik eine gruppe von hypothesentests mit chi quadrat verteilter testprüfgröße.

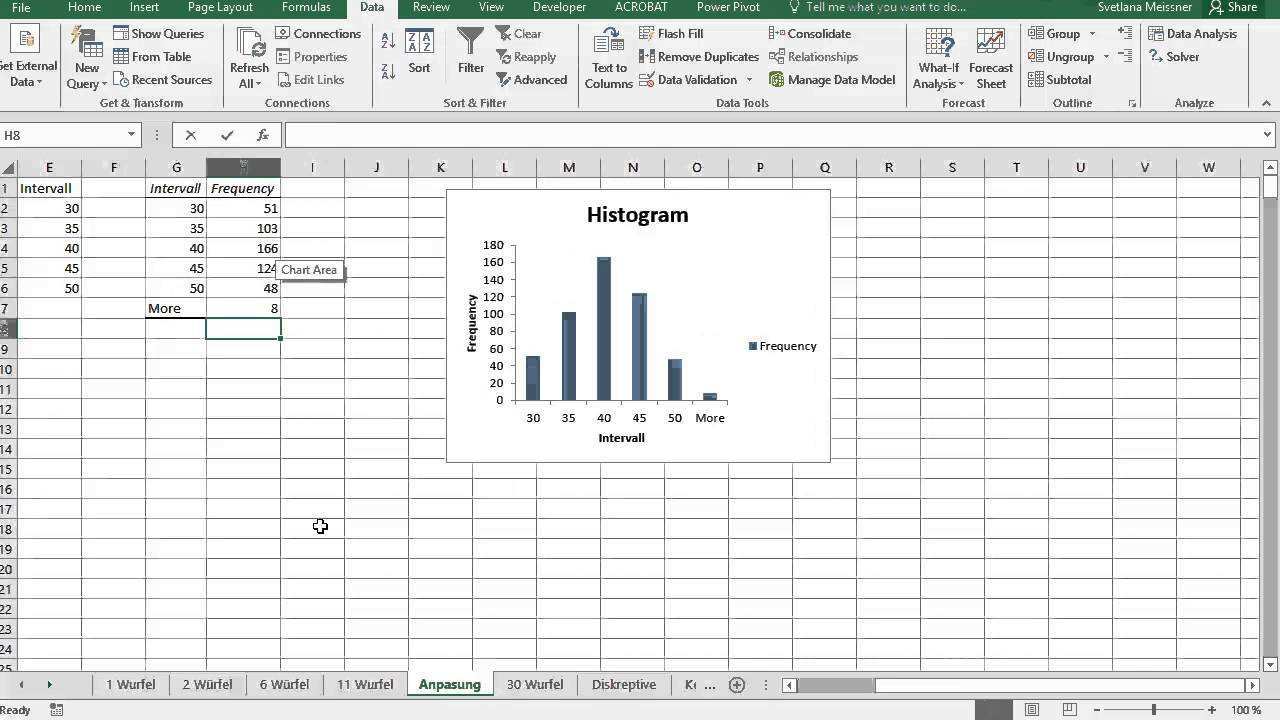
In der verteilungstabelle musst du daher in der spalte mit dem wert 0 950 nachschlagen. Hier wird geprüft ob vorliegende daten auf eine bestimmte weise verteilt sind. Ein 90 faches würfeln hat zu folgenden dargestellten absoluten häufigkeiten geführt. Häufigkeit der augenzahl beim würfelwurf.