Bernoulli Gleichung Beispiel

Die bernoulli gleichung beispiel für inkompressible strömung ist der energieerhaltungssatz in der strömungsmechanik fluiddynamik hydrodynamik.

Bernoulli gleichung beispiel. Wichtige anwendungsbeispiele sind die behandlung des hydrodynamischen paradoxons der ausfluß aus öffnungen sowie die grundlagen für verschiedene formen der druckmessung in strömungen. Die bernoulli gleichung die auch als gesetz von bernoulli oder als satz von bernoulli bezeichnet wird ist eine aussage über strömungen nach bernoulli und venturi. In diesem zusammenhang würde man es als treffer bezeichnen wenn man kopf hätte und als niete bei zahl oder auch andersherum. Bei einem bernoulli prozess gibt es nur zwei mögliche ergebnisse.

Dabei zähle eine schwarze kugel als treffer und eine weiße kugel als niete. 0 das ereignis tritt nicht ein. Die bernoullische gleichung ist eine der am häufigsten angewandten gleichungen der strömungsmechanik da sie den energieerhaltungssatz für flüssigkeiten ausdrückt. Wie wir sehen werden können sehr viele aufgabenarten als bernoulli prozess gedeutet werden und damit mit der bernoulli kette berechnet werden.

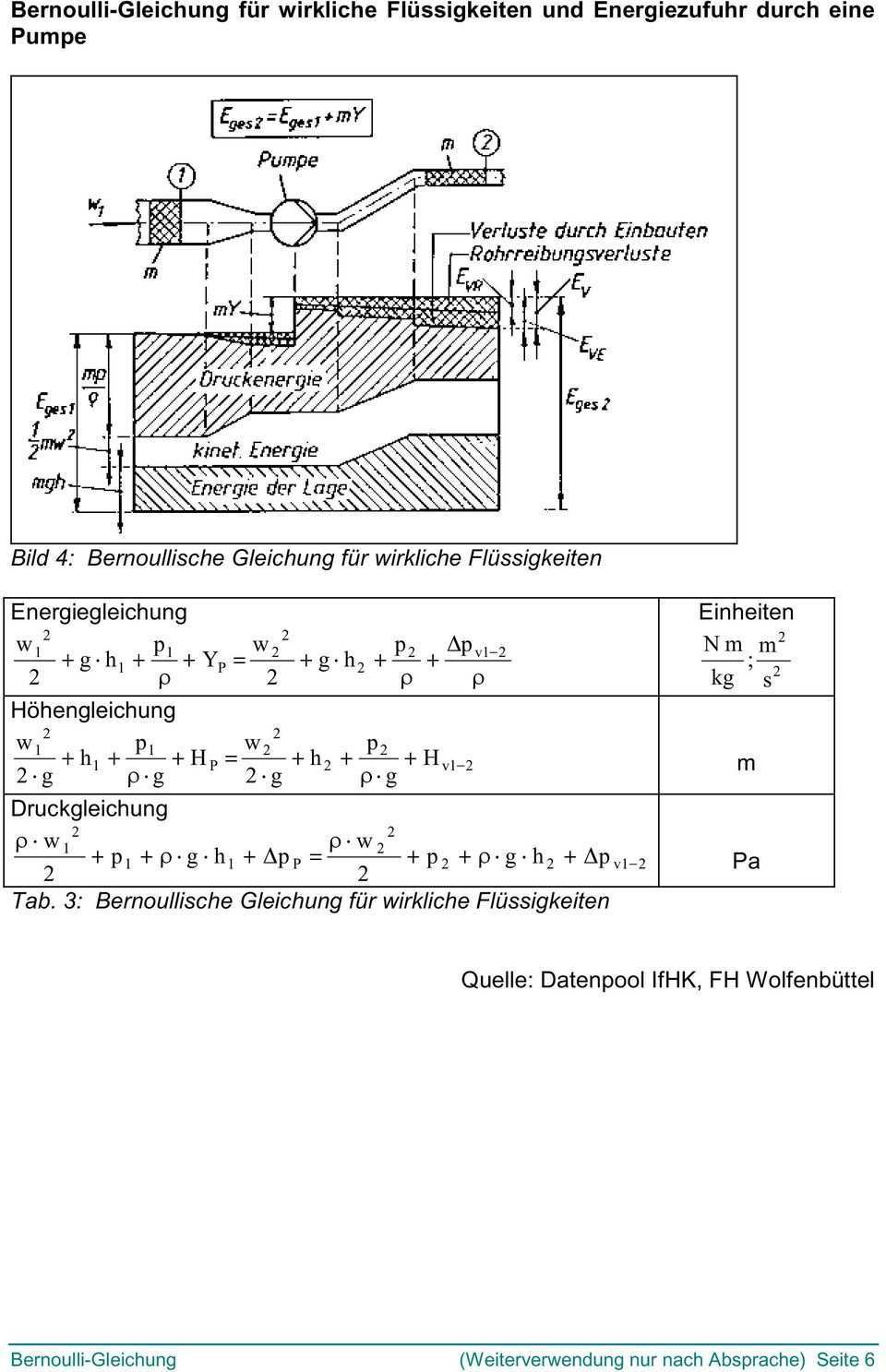
Die resultierende gleichung die als erweiterte bernoulli gleichung bezeichnet wird ist sehr nützlich bei der lösung der meisten flüssigkeitsströmungsprobleme. Beispiele für bernoulli versuchen sind. Eine faire münze hat die wahrscheinlichkeit von 0 5 oder 50 per definition. 1 das ereignis tritt ein.

H höhe über dem referenzniveau m v durchschnittliche geschwindigkeit der flüssigkeit m s. Ein beispiel für eine bernoulli kette der länge drei wäre das dreimalige ziehen mit zurücklegen aus einer urne mit nur schwarzen und weißen kugeln. Fasst man den höhenunterschied zu zusammen ergibt sich die formel nach torricelli zu. Die bernoulli differentialgleichung ist eine dgl erster ordnung und hat die gestalt y f x y g x y α y f x y g x y alpha y f x y g x y α α 1 alpha neq 1 α 1.

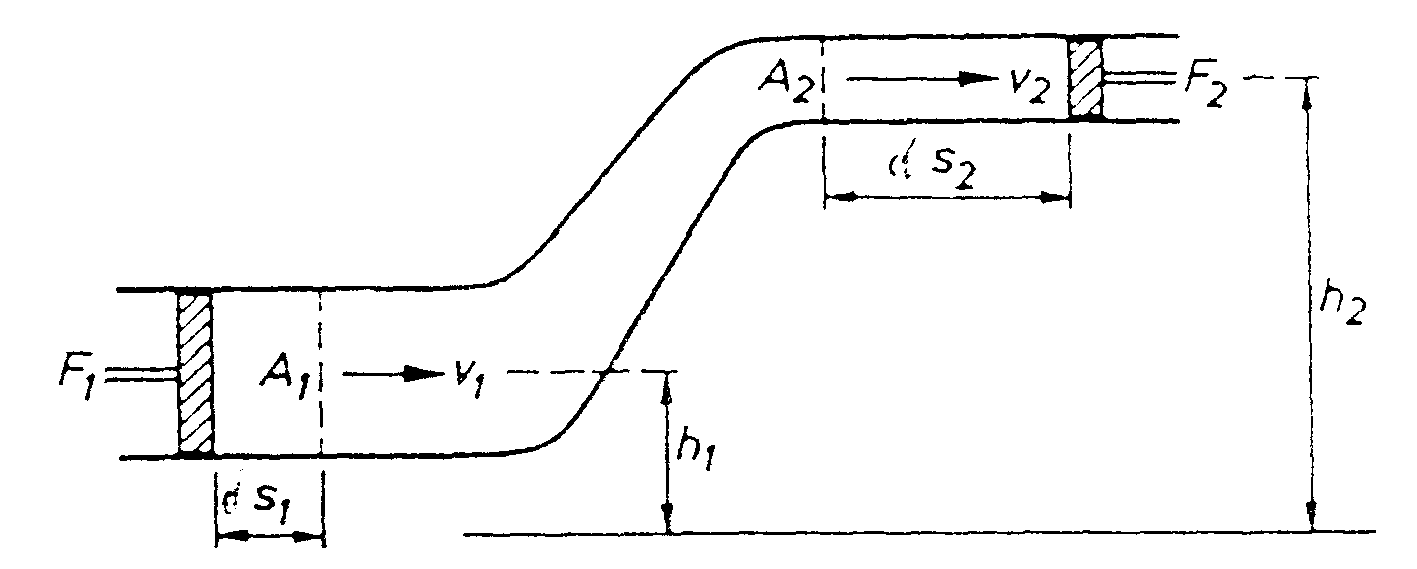
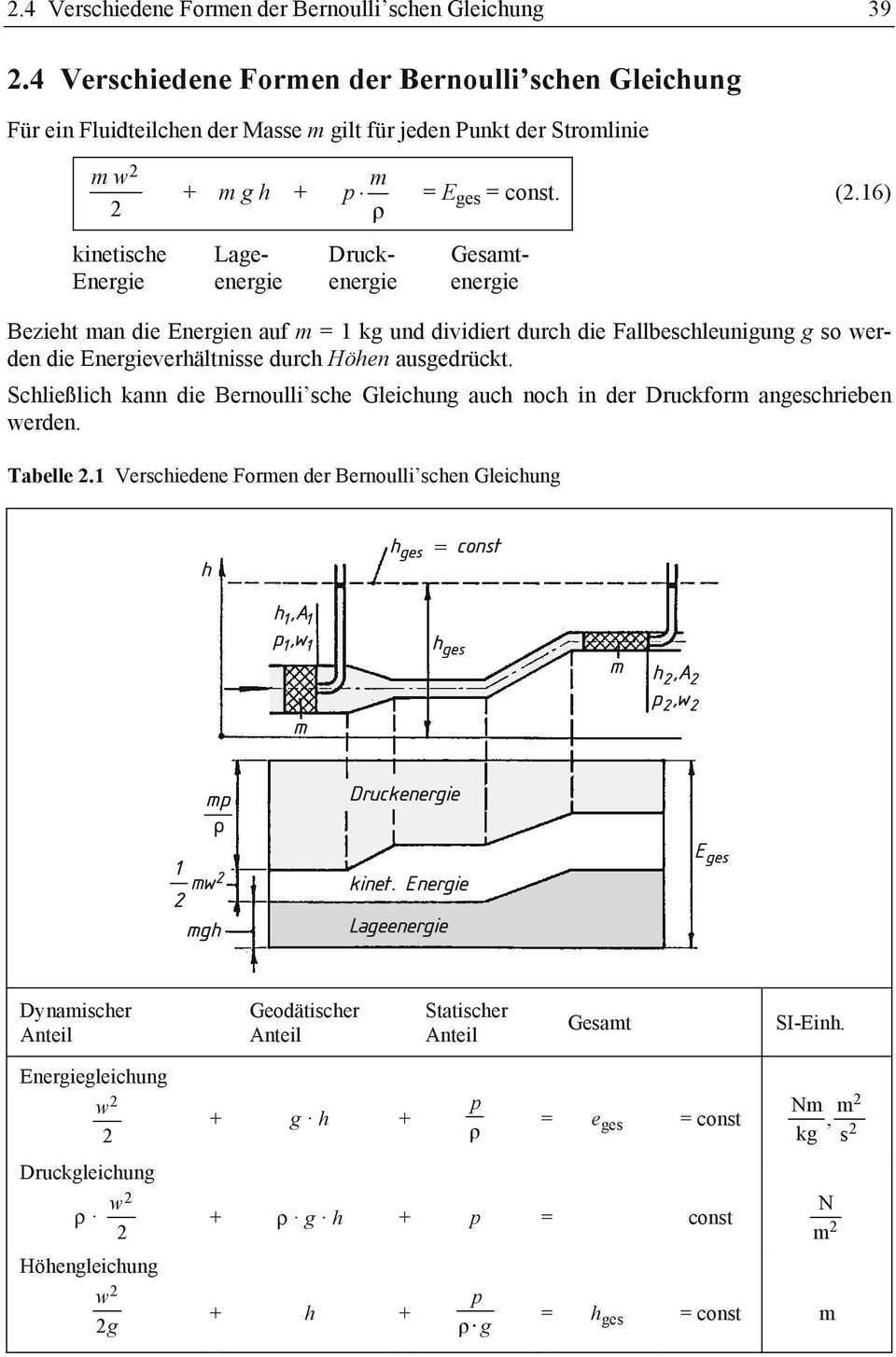
Die herleitung der bernoulli gleichung aus den navier stokes gleichungen führt auf die allgemeine bernoulli gleichung in der form u 1 2 2 p 1 v 1 u 2 2 2 p 2 v 2 η 1 2 u t d x displaystyle frac u 1 2 2 p 1 v 1 frac u 2 2 2 p 2 v 2 eta int 1 2 frac partial vec u partial t cdot mathrm d vec x. Die folgende gleichung ist eine form der erweiterten bernoulli gleichung. Die theorie über diese im wesentlichen eindimensionalen strömungen entlang eines stromfadens wurde im 18. 4 1 2 v 1 p 1 ρ g h 1 1 2 v 2 p 2 ρ g h 2 mit unter annahme eines hinreichend großen reservoirs.